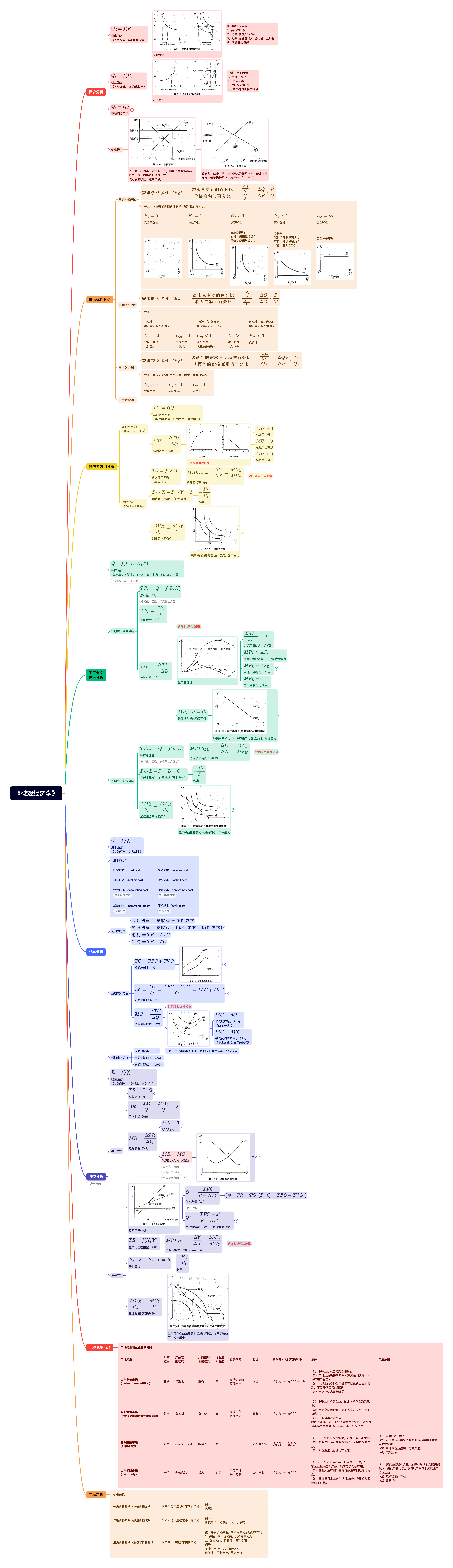
《微观经济学》读书笔记

维基百科对图(Graph)的定义:
A graph is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically.
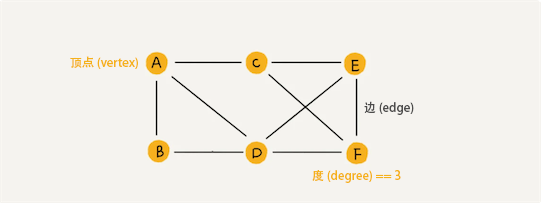
任何两个顶点(vertex)之间都有边(edge)的无向图称为无向完全图。一个具有 n 个顶点的无向完全图的边数为:
$$
C^2_n=n(n-1)/2
$$
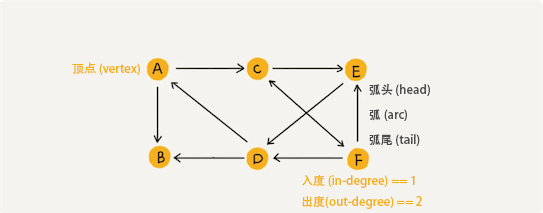
任何两个顶点(vertex)之间都有弧(arc)的有向图称为有向完全图。一个具有 n 个顶点的有向完全图的弧数为:
$$
P^2_n=n(n-1)
$$
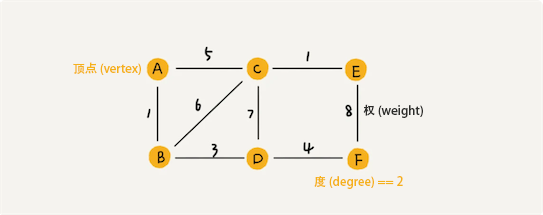
边或弧上带有权值的图,也称为网(network)。
维基百科对网(network)的定义:
In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes (e.g. names).
图(graph)是高度抽象后的逻辑结构,而网(network)在此之上可以通过在顶点(vertex)和边(edge)上增加属性来包含更多的信息,更偏重于对实际问题的建模。
https://en.wikipedia.org/wiki/Glossary_of_graph_theory
What’s the difference between Adjacency and Connectivity ?
在无向图中,邻接是点与点或者边与边之间的关系。在无向图中,如果两个点之间至少有一条边相连,则称这两个点是邻接的。同样,如果两条边有共同的顶点,则两条边也是邻接的。关联是点与边之自的关系。一个点如果是一条边的顶点之一,则称为点与该边关联。
维基百科对矩阵(Matrix)的定义:
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
维基百科对矩阵(Matrix)的定义 2:
数学上,一个 $m×n$ 的矩阵是一个由 $m$ 行(row)$n$ 列(column)元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。
矩阵(Matrix)是很多科学计算问题研究的对象,矩阵可以用二维数组来表示。
图最直观的一种存储方法就是,邻接矩阵(Adjacency Matrix)。
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
定义如下:
设 $G=(V,\ E)$ 是一个图,其中 $V={v_0,\ v_1,\ …\ ,\ v_{n-1}}$,那么 $G$ 的邻接矩阵 $A$ 定义为如下的 $n$ 阶方阵:
$$
A_{[i][j]}=
\begin{cases}
1& {若\ (v_i,\ v_j)\ 或\ <v_i,\ v_j>\ ∈\ E}\
0& {若\ (v_i,\ v_j)\ 或\ <v_i,\ v_j>\ ∉\ E}
\end{cases}
$$
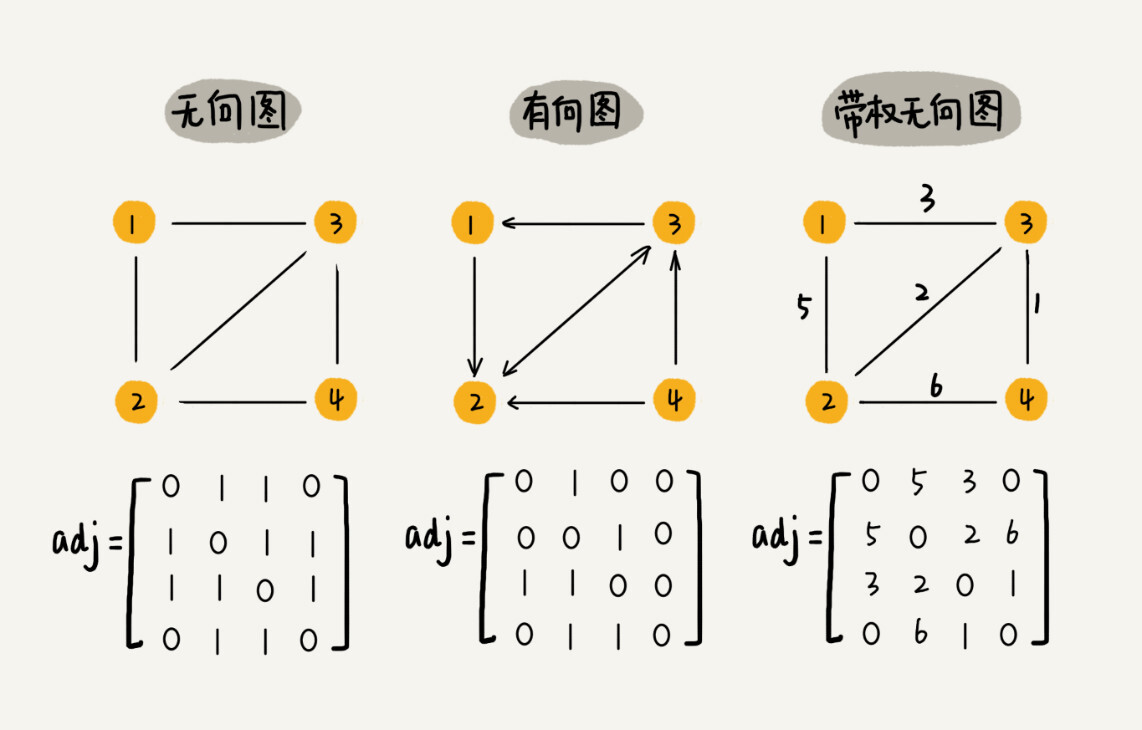
可见,若无向图 $G$ 中有 $n$ 个顶点 $m$ 条边,采用邻接矩阵存储,则该矩阵中非 0 元素的个数为:
$$
2m
$$
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。为什么这么说呢?
对于无向图来说,如果 $A_{[i][j]}$ 等于 1,那 $A_{[j][i]}$ 也肯定等于 1。实际上,我们只需要存储一个就可以了。也就是说,无向图的二维数组中,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
上面描述的是一类特殊矩阵:
若一个 $n$ 阶方阵 $A$ 中的元素满足下述条件:
$$
a_{ij}=a_{ji} \quad (0≤i,\ j≤n-1)
$$
则 $A$ 称为对称矩阵(Symmetric Matrix)。
In the mathematical discipline of linear algebra, a symmetric matrix is a square matrix that is equal to its transpose.
对称矩阵可以压缩存储:对称矩阵有近一半的元素可以通过其对称元素获得,为每一对对称元素只分配一个存储单元,则可将 $n^2$ 个元素压缩存储到含有 $n(n+1)/2$ 个元素的一维数组中。
以对称矩阵的主对角线为界,上(下)半部分是一个固定的值(如 0),这样的矩阵称为:上三角矩阵(Upper Triangular Matrix)或下三角矩阵(Lower Triangular Matrix)。
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix. A square matrix is called lower triangular if all the entries above the main diagonal are zero. Similarly, a square matrix is called upper triangular if all the entries below the main diagonal are zero.
如果我们存储的是稀疏矩阵(Sparse Matrix),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户,对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多,一般也就三五百个而已。如果我们用邻接矩阵来存储,那绝大部分的存储空间都被浪费了。
这里描述的是一类「非零元素个数很少的矩阵」,即稀疏矩阵(Sparse Matrix)。
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero.
稀疏矩阵可以压缩存储,使用三元组表示法:$(i,\ j,\ a_{ij})$。
总结,邻接矩阵的存储方法的优点:
- 首先,邻接矩阵的存储方式简单、直接,因为基于数组,所以在获取两个顶点的关系时,就非常高效。
- 其次,用邻接矩阵存储图的另外一个好处是方便计算。这是因为,用邻接矩阵的方式存储图,可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个 Floyd-Warshall 算法,就是利用矩阵循环相乘若干次得到结果。参考:《矩阵运算及其运算规则》
此外,针对邻接矩阵比较浪费存储空间的缺点,解决方案:
- 不带权的无向图的邻接矩阵,一定是一个对称矩阵,因此可以转为三角矩阵之后进行压缩存储。
- 有向图、带权图的邻接矩阵,一般都不是一个对称矩阵。但如果是一个稀疏矩阵,可以使用三元组表示法进行压缩存储。
邻接表(Adjacency List) 的定义:
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.
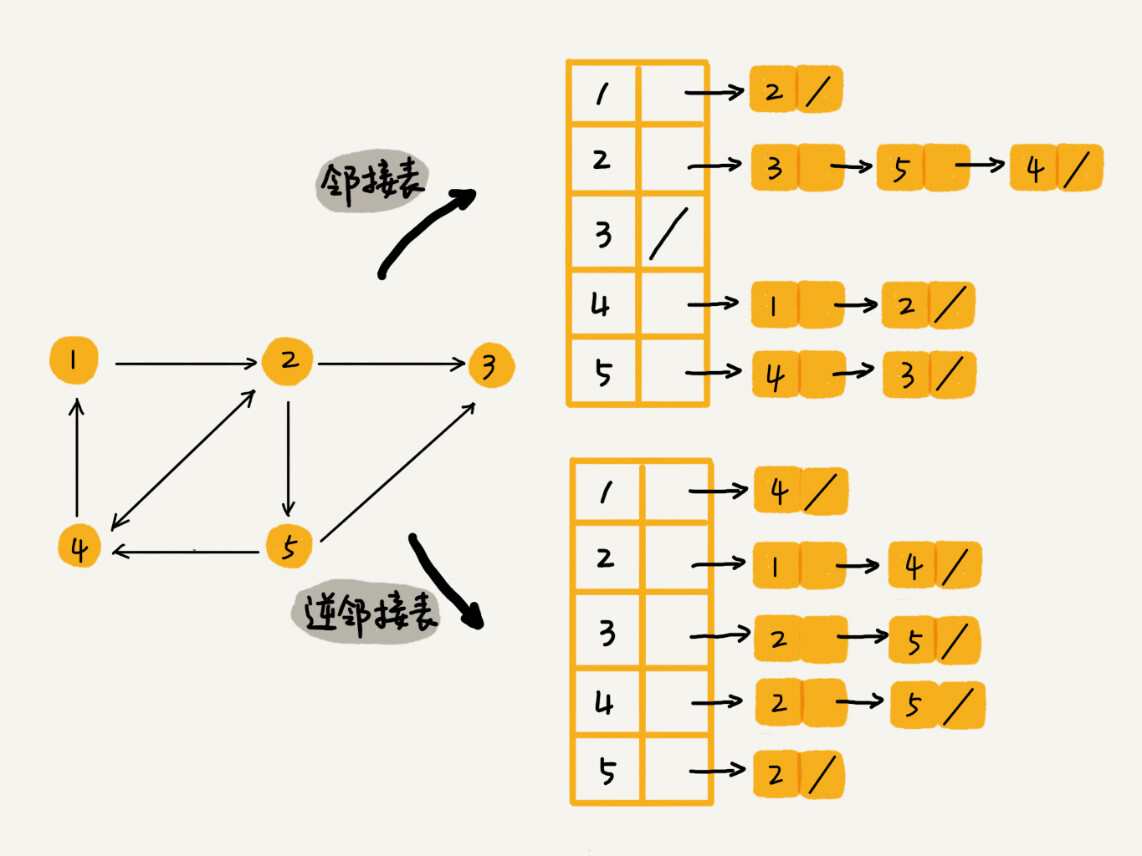
还记得我们之前讲过的时间、空间复杂度互换的设计思想吗?邻接矩阵存储起来比较浪费空间,但是使用起来比较节省时间。相反,邻接表存储起来比较节省空间,但是使用起来就比较耗时间。
就像图中的例子,如果我们要确定,是否存在一条从顶点 2 到顶点 4 的边,那我们就要遍历顶点 2 对应的那条链表,看链表中是否存在顶点 4。而且,我们前面也讲过,链表的存储方式对缓存不友好。所以,比起邻接矩阵的存储方式,在邻接表中查询两个顶点之间的关系就没那么高效了。
在基于链表法解决冲突的散列表中,如果链过长,为了提高查找效率,我们可以将链表换成其他更加高效的数据结构,比如平衡二叉查找树等。所以,我们也可以将邻接表同散列表一样进行 “改进升级”。
我们可以将邻接表中的链表改成平衡二叉查找树。实际开发中,我们可以选择用红黑树。这样,我们就可以更加快速地查找两个顶点之间是否存在边了。当然,这里的二叉查找树可以换成其他动态数据结构,比如跳表、散列表等。除此之外,我们还可以将链表改成有序动态数组,可以通过二分查找的方法来快速定位两个顶点之间否是存在边。
https://en.wikipedia.org/wiki/Graph_traversal
图上的搜索算法,最直接的理解就是,在图中找出从一个顶点出发,到另一个顶点的路径。具体方法有很多,比如两种最简单、最 “暴力” 的深度优先、广度优先搜索,还有 A*、IDA* 等启发式搜索算法。
连通图的两种搜索方式:
| 邻接矩阵 | 邻接表 | |
|---|---|---|
| 深度优先搜索 | 栈(LIFO)实现($O(n+e)$) | |
| 广度优先搜索 | 队列(FIFO)实现 |
https://en.wikipedia.org/wiki/Depth-first_search
深度优先搜索(Depth-first search, DFS)类似于树的先序遍历。
想象成“走迷宫”的过程。
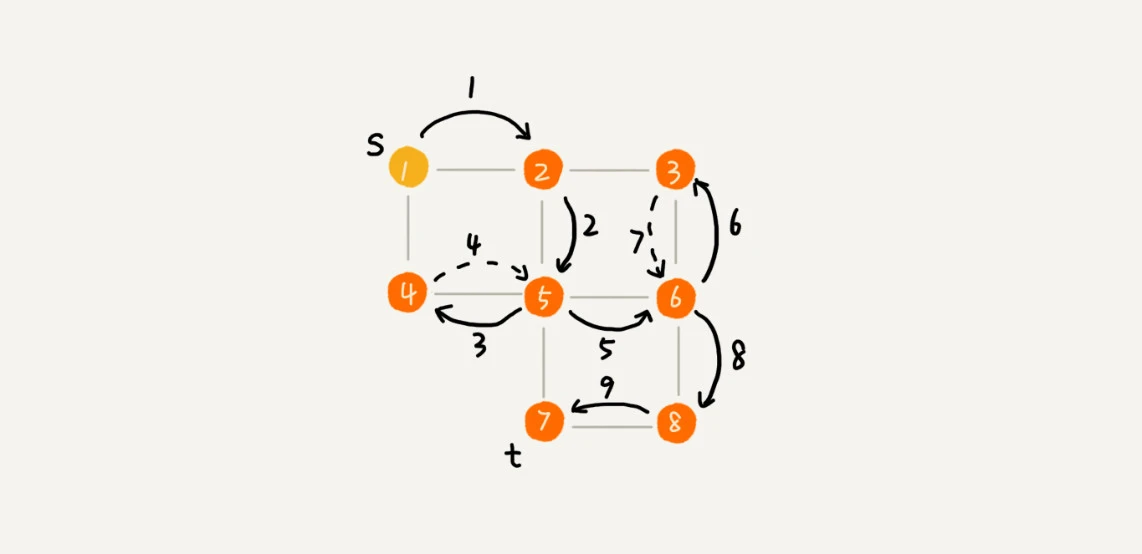
实际上,深度优先搜索用的是一种比较著名的算法思想——回溯思想。这种思想解决问题的过程,非常适合用递归来实现。而递归的本质就是压栈与出栈操作。
深度优先搜索的栈(LIFO)实现,过程如下图,将压栈 push 的顶点序列输出即可。

https://en.wikipedia.org/wiki/Breadth-first_search
广度优先搜索(Breadth-first search, BFS)类似于树的层次遍历。
想象成 “地毯式搜索” 层层推进的过程。
广度优先搜索的队列(FIFO)实现,过程如下:
首先顶点入队,并输出。
然后顶点出队。
将出队顶点相连的所有顶点依次入队,并输出。
重复 2、3 两步,直到所有顶点输出为止,最终结果不唯一。

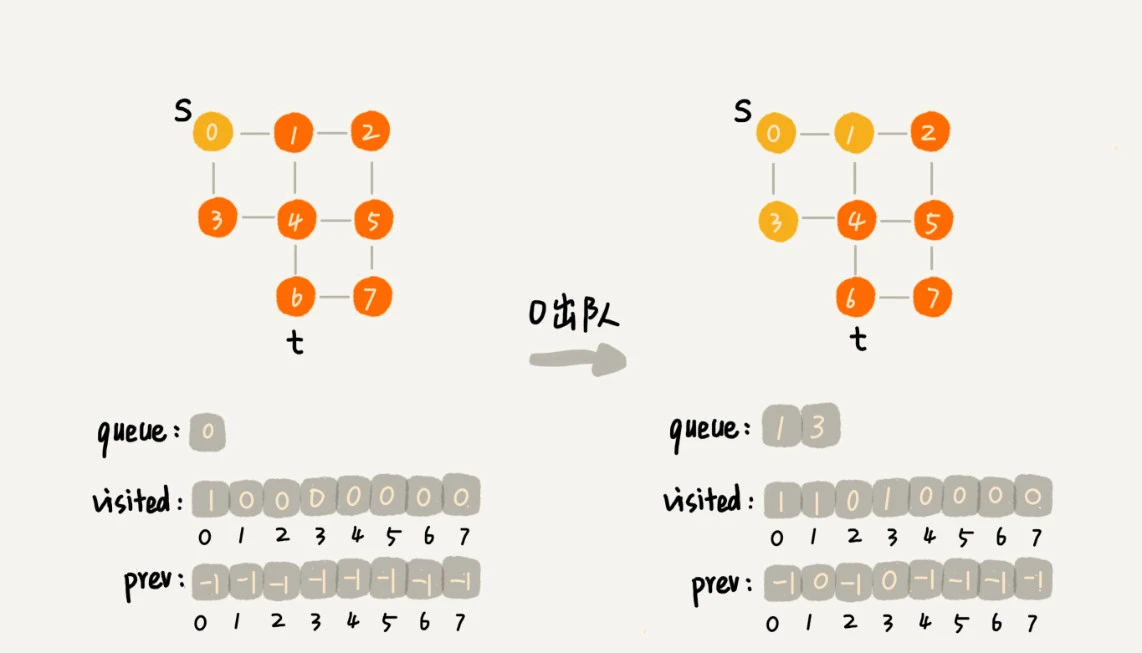
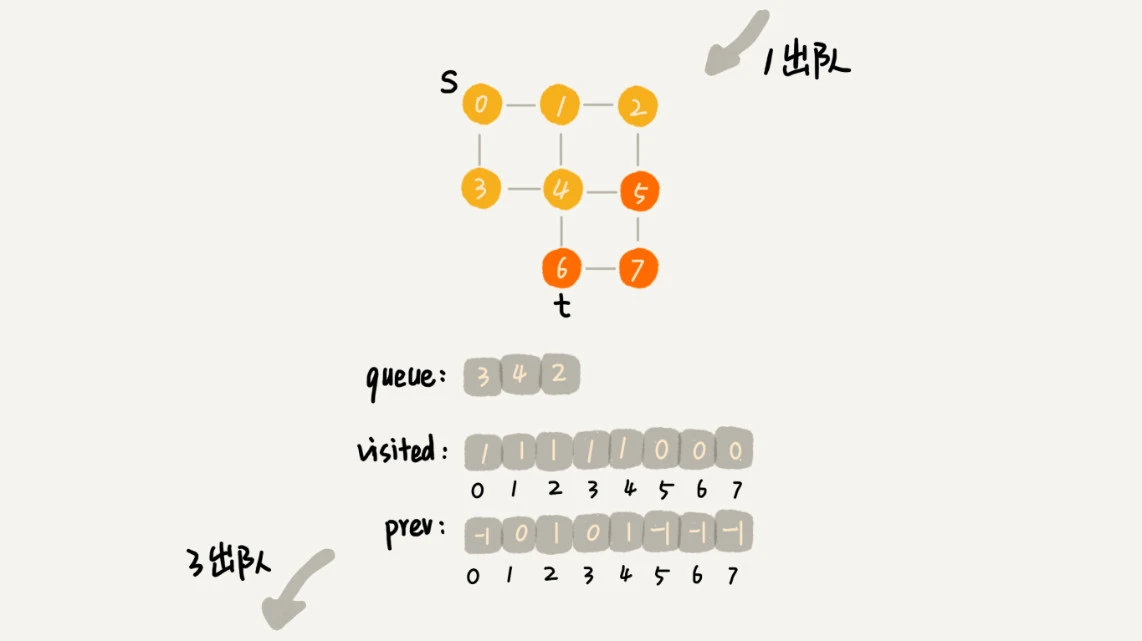
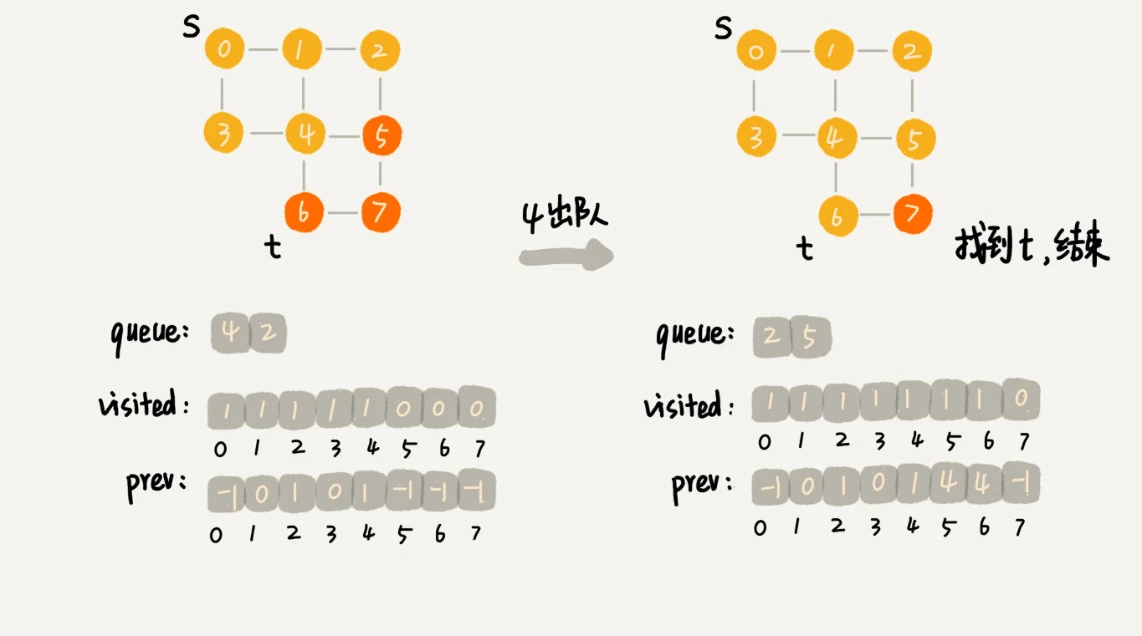
无向图中的极大连通子图(Maximal connected subgraph)称为原图的连通分量(Connected Components)。
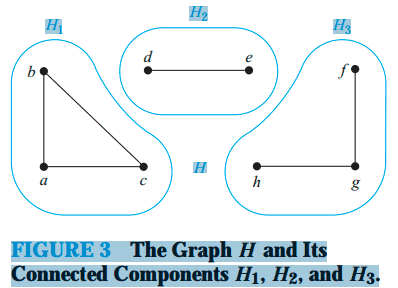
连通图只有一个极大连通子图,就是它本身。
如果无向图中,任意两个顶点都连通,称为连通图(Connected Graph)。如下图:

如果连通图中,边上有权值,称为连通网(Connected Network)。如下图:

连通图的一次遍历所经过的点和边的集合,构成一棵生成树(Spanning Tree)。
一个连通图的生成树,是含有该连通图的全部顶点的一个极小连通子图(Minimum connected subgraph)。
一个具有 $n$ 个顶点的连通图,它的生成树的边数为 $n-1$。
连通图的遍历序列不是唯一的,所以能得到不同的生成树。其中权值总和最小的生成树,称为最小生成树(Minimum Spanning Tree, MST)。如下图:
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible.
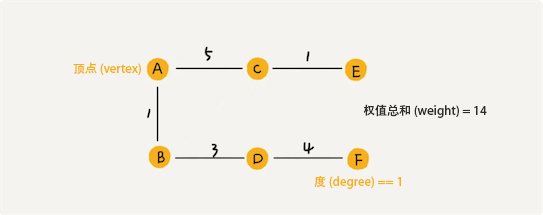
最小生成树的准则:
n-1 条边来联结网络中的 n 个顶点;最小生成树的应用:规划出总长度最小的网络
https://en.wikipedia.org/wiki/Prim%27s_algorithm
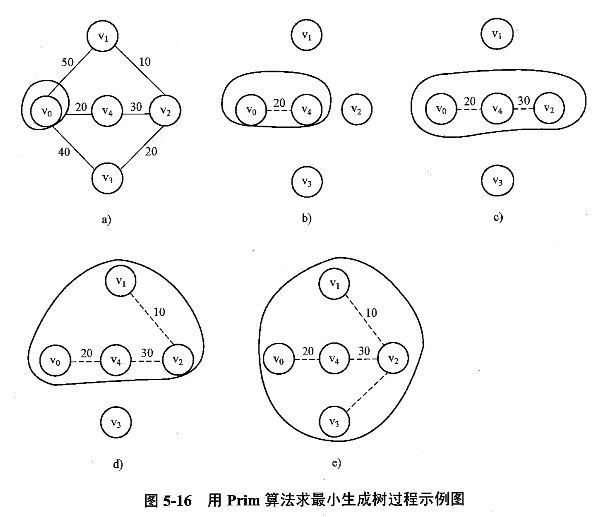
假设 $N=(V,\ E)$ 是连通网,$TE$ 是 $N$ 上最小生成树中边的集合:
初始态:$U={u_0},\ (u_0∈V),\ TE={}$
在所有 $u∈U,\ v∈V-U$ 的边 $(u,\ v)∈E$ 中找一条代价最小的边 $(u,\ v_0)$ 并入集合 $TE$,
同时 $v_0$ 并入 $U$
重复 2,直到 $U=V$
形象化理解:由点找边再找点的过程。

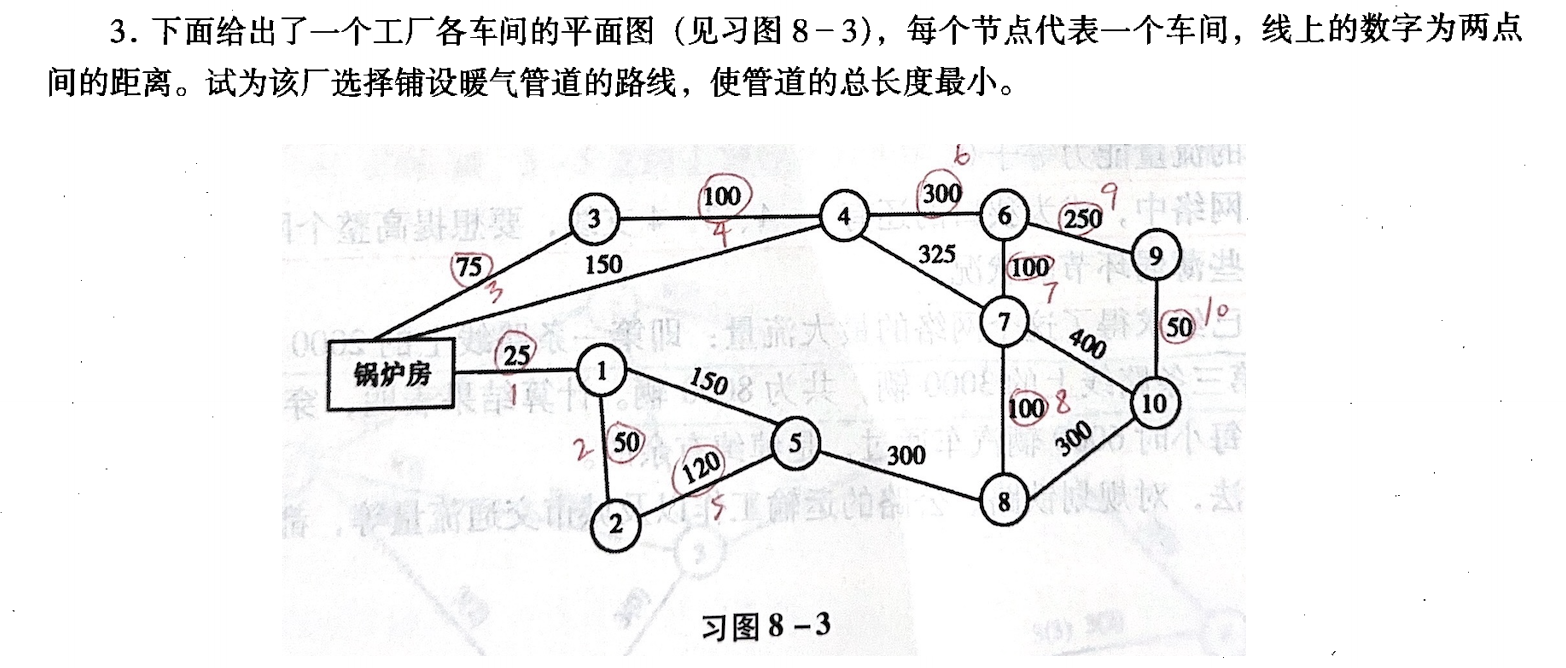
📝 习题 📝
https://en.wikipedia.org/wiki/Kruskal%27s_algorithm
假设 $N=(V,\ E)$ 是连通网
形象化理解:由边找点。
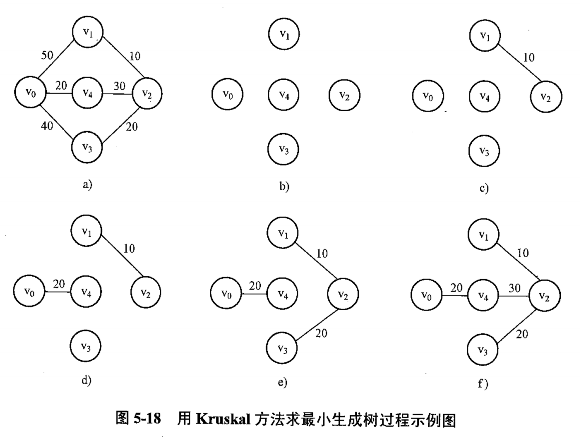

在图论中,最短路径问题是在连通图中寻找两个顶点之间的一条路径,使得其组成边的权重(如时间、距离、费用等)之和最小化的问题。
最短路径的应用:
最短路径的计算方法:
最短路径算法还有很多,比如 Bellford 算法、Floyd 算法等等。
从终点开始,逐步逆向推算。(从终点到起点的逆向回溯过程。)
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
《44 | 最短路径:地图软件是如何计算出最优出行路径的?》
📝 习题 📝
| 目的地 | 起点:甲 | 前驱 | 最短路径 |
|---|---|---|---|
| 1 ✅(2️⃣) | 33 | 甲 | 甲 - 1 |
| 2 ✅(1️⃣) | 27 | 甲 | 甲 - 2 |
| 3 ✅(4️⃣) | 52 | 甲 | 甲 - 3 |
| 4 ✅(3️⃣) | 47 | 2 | 甲 - 2 - 4 |
| 5 ✅(6️⃣) | 甲 - 2 - 4 - 乙 - 5 | ||
| 乙 ✅(5️⃣) | 甲 - 2 - 4 - 乙 |
https://en.wikipedia.org/wiki/A*_search_algorithm
《49 | 搜索:如何用 A * 搜索算法实现游戏中的寻路功能?》
https://en.wikipedia.org/wiki/Maximum_flow_problem
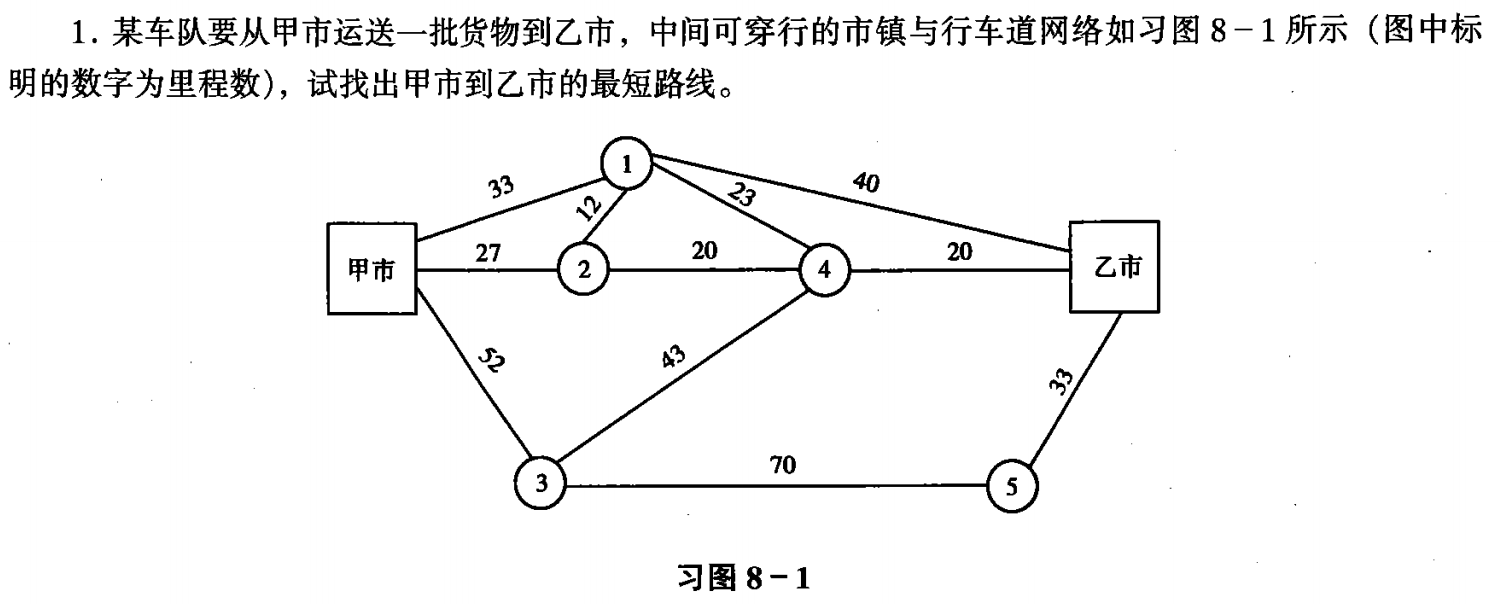
当以物体、能量或信息等作为流量流过网络时,怎样使流过网络的流量最大,或者使流过网络的流量的费用或时间最小。通常,把设计这样的流量模型问题,叫作网络的流量问题。
最大流量问题,就是在一定条件下,要求流过网络的流量为最大的问题。
📝 习题 📝
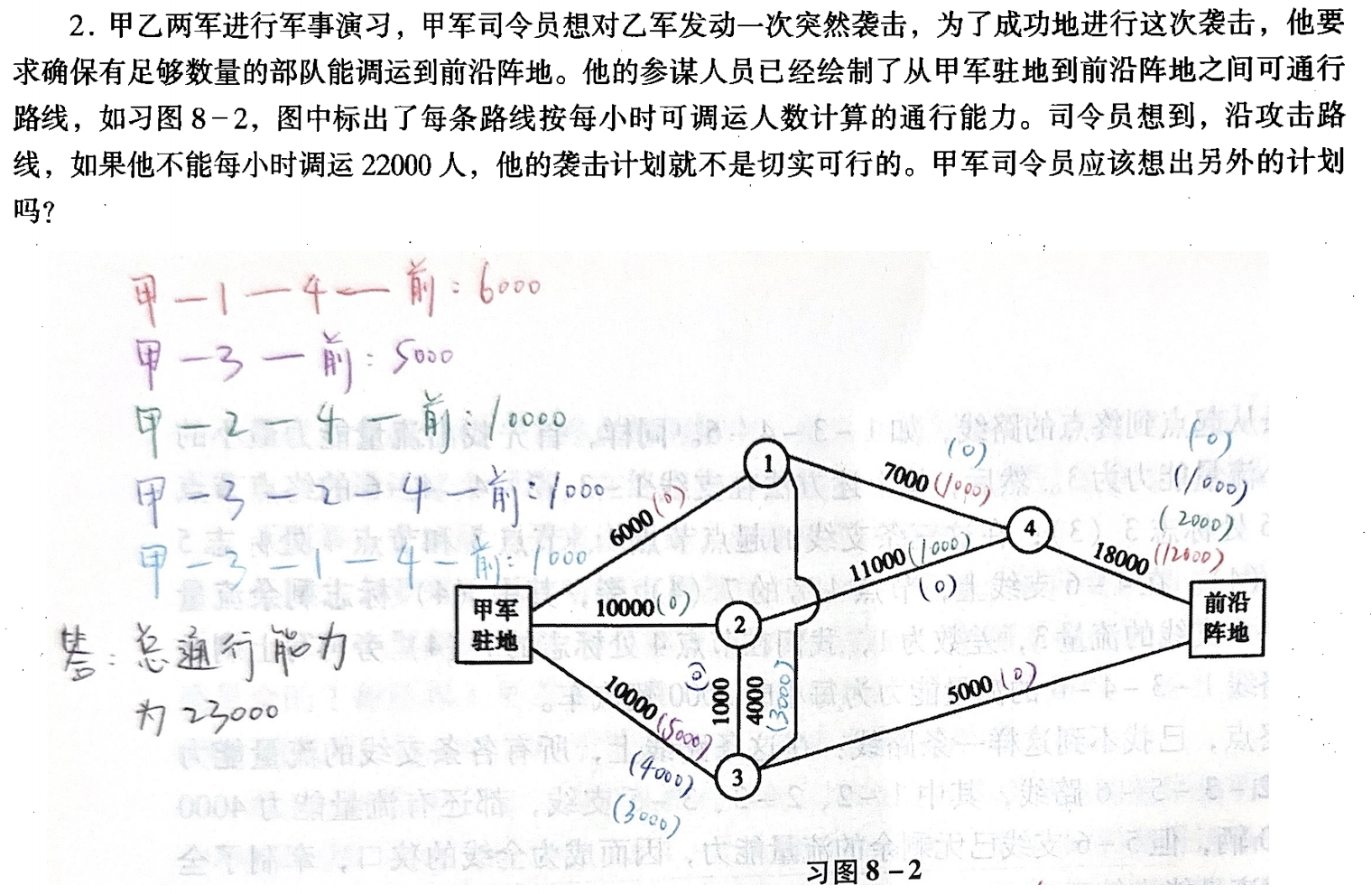
拓扑排序算法:
重复 1、2 两步,直到所有顶点输出为止,最终结果不唯一。
设某有向图中有 n 个顶点和 e 条边,进行拓扑排序时,总的计算时间为 $O(n+e)$。
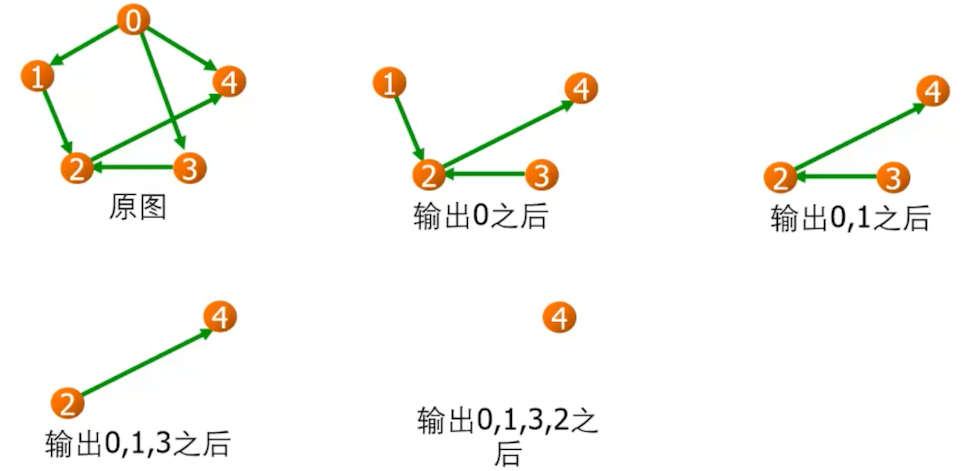
https://en.wikipedia.org/wiki/Topological_sorting
图的两种存储结构,在社交应用的优缺点对比如下。例如在微博(有向图)中,设我为 $v_i$,ta 为 $v_j$:
| 需求 | 邻接矩阵 | 邻接表 A、逆邻接表 R |
|---|---|---|
| 我关注的人 | $A_{[i][0-n]}$ | $A_{[i]}$ |
| 我的粉丝(关注我的人) | $A_{[0-n][i]}$ | $R_{[i]}$ |
| 我关注 ta | $A_{[i][j]}$ = 1 | insert($A_{[i]}$, $v_j$) && insert($R_{[j]}$, $v_i$) |
| 我取消关注 ta | $A_{[i][j]}$ = 0 | delete($A_{[i]}$, $v_j$) && delete($R_{[j]}$, $v_i$) |
| 我是否关注 ta | $A_{[i][j]}$ == 1 | exist($A_{[i]}$, $v_j$) |
| ta 的粉丝是否有我 | $A_{[i][j]}$ == 1 | exist($R_{[j]}$, $v_i$) |
基于上述存储结构,可以进一步实现如下需求(以邻接表为例):
1 | # 求共同关注 |
https://en.wikipedia.org/wiki/Knowledge_graph
https://en.wikipedia.org/wiki/Graph_theory
https://en.wikipedia.org/wiki/Network_theory
维基百科 Tree (data structure) 的相关术语:
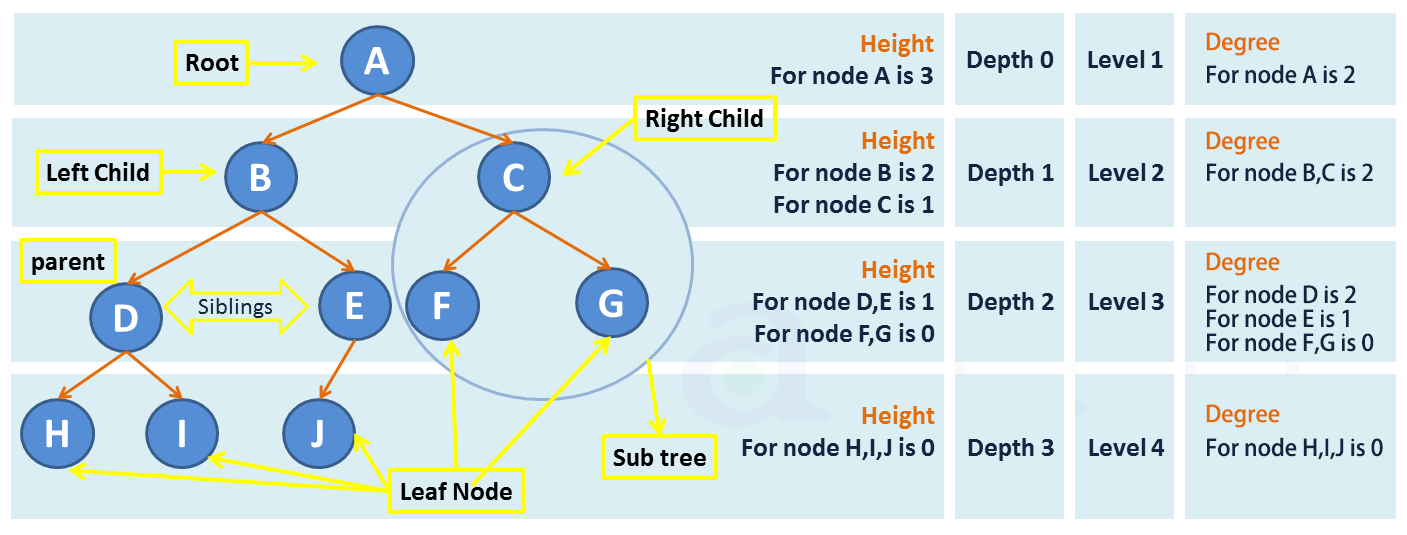
结点(Node):包含一个数据元素及若干指向其子树的分支。
结点的度(Degree of node):
For a given node, its number of children. A leaf has necessarily degree zero.
树的度(Degree of tree):
The degree of a tree is the maximum degree of a node in the tree.
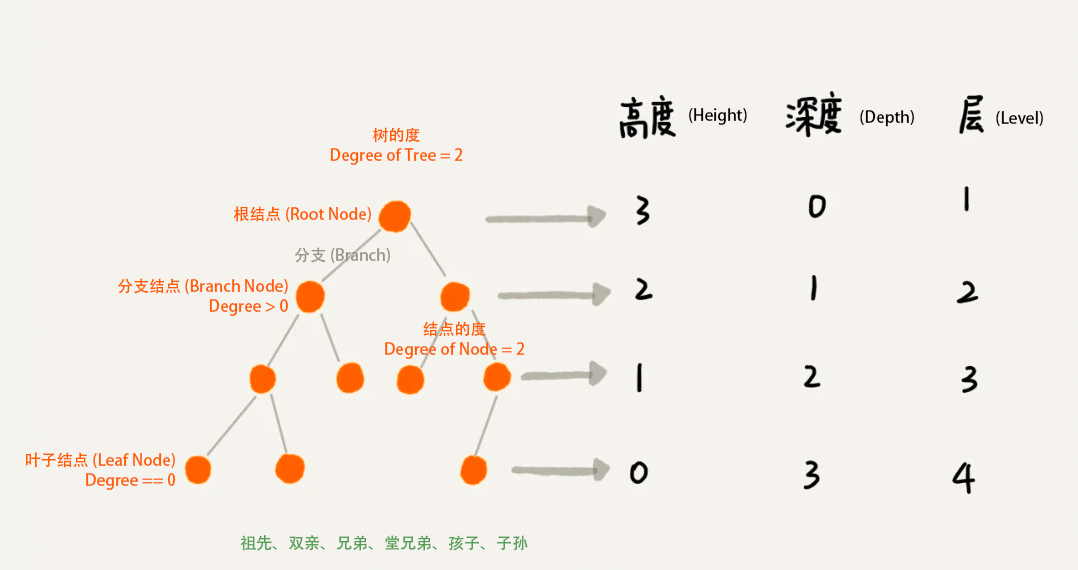
高度(Height)、深度(Depth):
The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree.
The depth of a node is the length of the path to its root (i.e., its root path).
When using zero-based counting, the root node has depth zero, leaf nodes have height zero, and a tree with only a single node (hence both a root and leaf) has depth and height zero. Conventionally, an empty tree (tree with no nodes, if such are allowed) has height −1.
参考:
https://www.baeldung.com/cs/tree-depth-height-difference
https://stackoverflow.com/questions/2603692/what-is-the-difference-between-tree-depth-and-height
有没有想过为啥有二叉树,而没有一叉树?实际上顺序表、链式表就是特殊的树,即一叉树实现。
二叉树的五种基本形态:
注意:一棵树(包括二叉树)的最少结点个数为 0(空树)。

二叉树的常见形态:
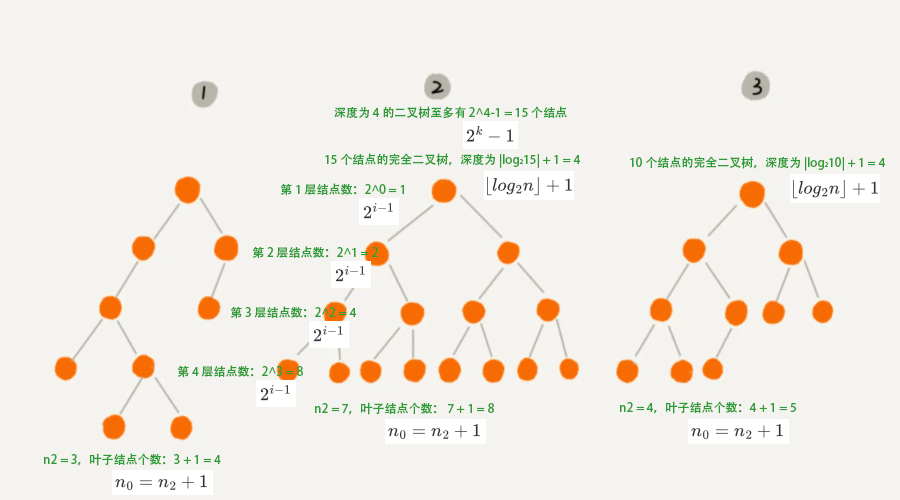
二叉树的通用性质:
性质 1:二叉树第 i (i ≥ 1) 层至多有 $2^{i-1}$ 个结点。
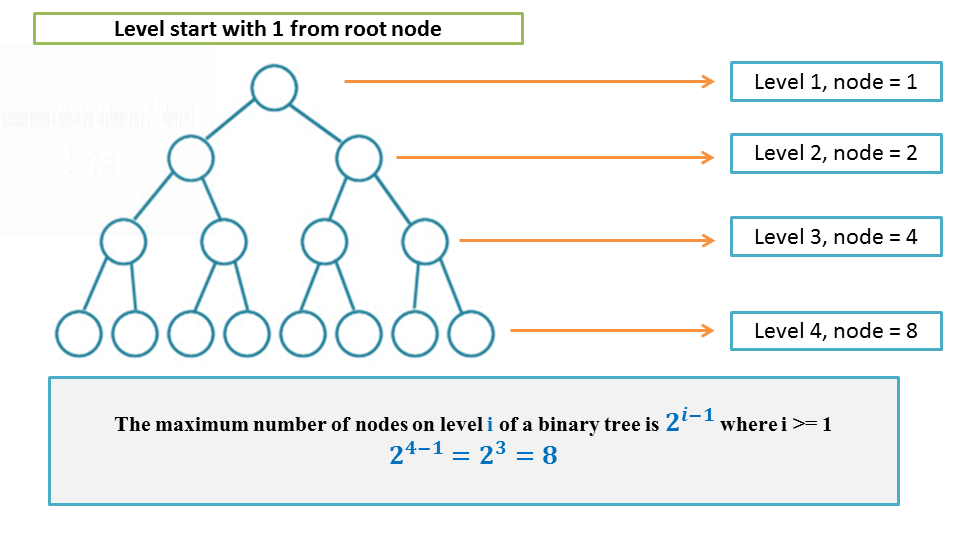
性质 2:深度为 k (k ≥ 1) 的二叉树至多有 $2^k-1$ 个结点。
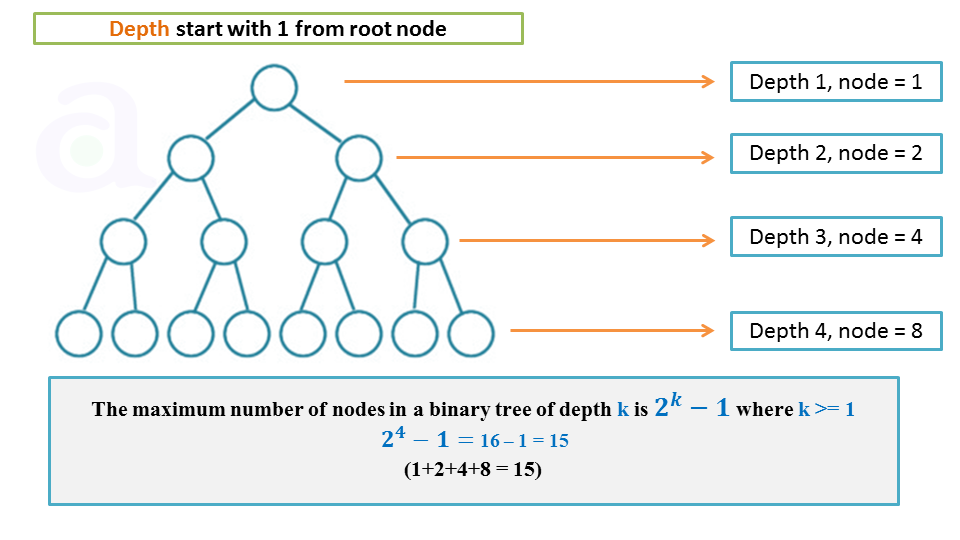
性质 3:二叉树中,若度数为 0 的叶子结点个数为 $n_0$,度数为 2 的结点个数为 $n_2$,则 $n_0 = n_2 + 1$。
若根节点的层数为 1,则具有 n 个结点的二叉树的最大高度为 n(即一叉树)。
参考:https://www.atnyla.com/tutorial/level-and-height-of-the-tree/3/392
下面介绍几种特殊的二叉树:
满二叉树的性质:
深度为 k (k ≥ 1) 的满二叉树,共有 $2^k-1$ 个结点。如下图和表格:
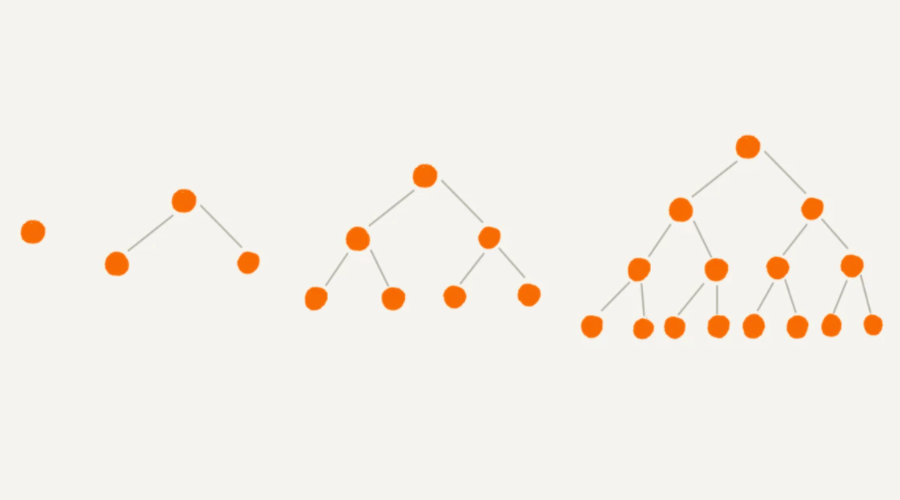
| $k=1$ | $k=2$ | $k=3$ | $k=4$ | |
|---|---|---|---|---|
| 结点总数 | $2^1-1=1$ | $2^2-1=3$ | $2^3-1=7$ | $2^4-1=15$ |
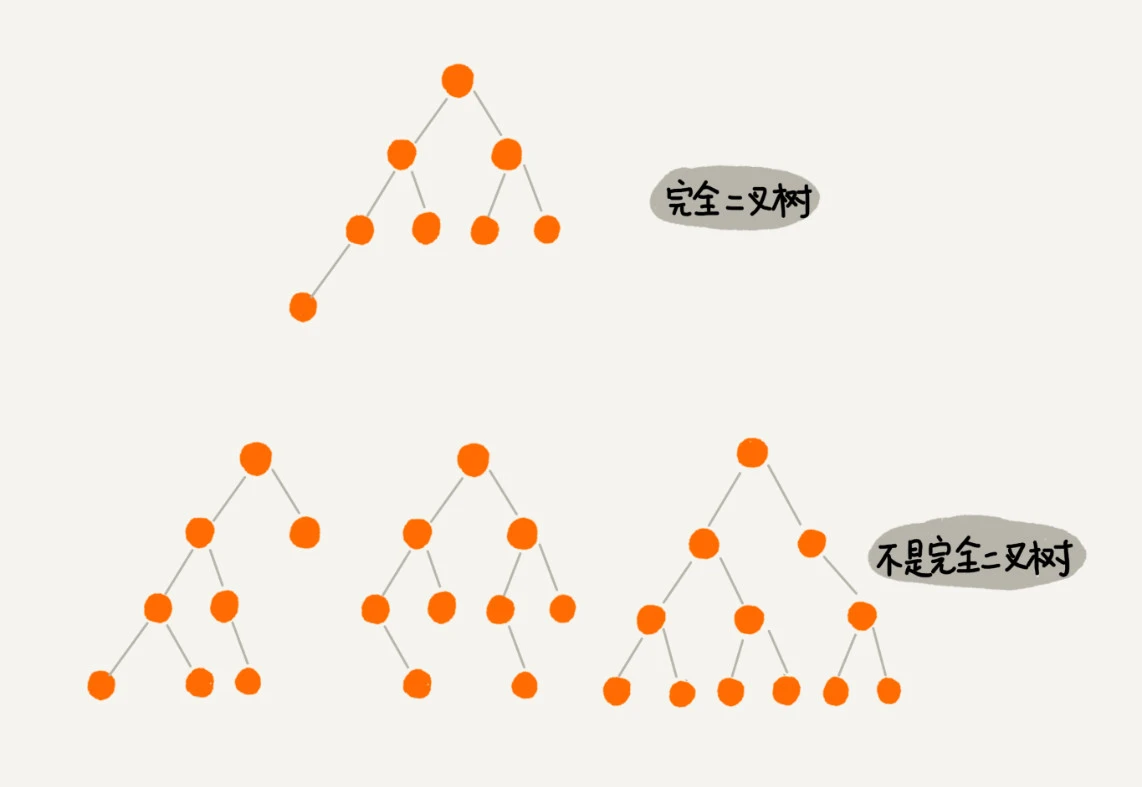
完全二叉树的性质:
含有 n 个结点的完全二叉树,深度为 $⌊log_2n⌋+1$。
深度为 k 的完全二叉树:
| $k=1$ | $k ≥ 2$ | |
|---|---|---|
| 最少结点数 | $2^{k-1}$ | $2^{k-1}$ |
| 最少叶子结点数 | $k$ | $2^{k-2}$ |
如下图和表格:

| $k=1$ | $k=2$ | $k=3$ | $k=4$ | |
|---|---|---|---|---|
| 最少结点数 | $2^{1-1}=1$ | $2^{2-1}=2$ | $2^{3-1}=4$ | $2^{4-1}=8$ |
| 最少叶子结点树 | 1 | $2^{2-2}=1$ | $2^{3-2}=2$ | $2^{4-2}=4$ |
含有 n 个结点的完全二叉树按层编号,则:
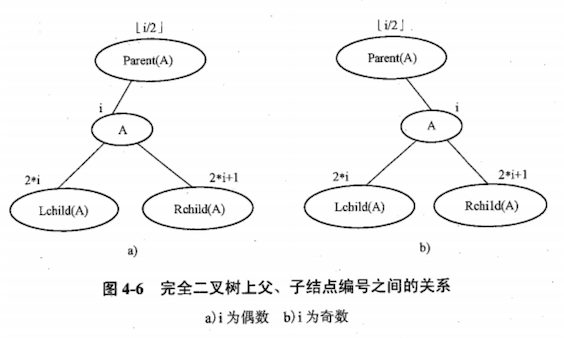
如果将完全二叉树按层编号,并以编号作为数组下标将结点存入一维数组中,则完全二叉树的顺序存储结构如下图:
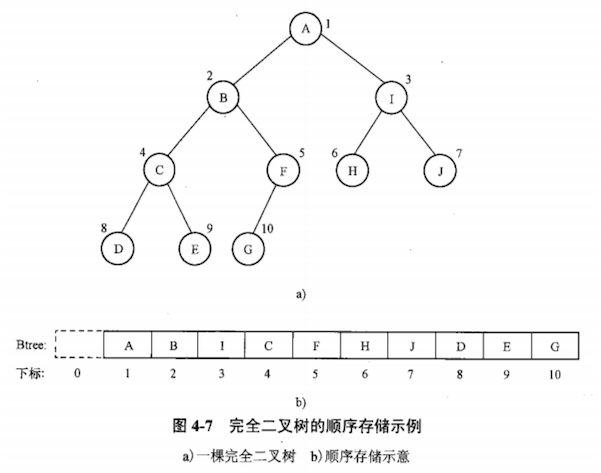
通过观察,完全二叉树按层编号之后,编号之间的关系满足下图的编号计算公式。

公式可以准确反映出结点之间的逻辑关系,可用于求某结点的父、子结点。(这一性质是二叉树顺序存储结构的基础)
但如果将非完全二叉树按层编号进行顺序存储,则无法套用编号计算公式求父、子结点:
| 优点 | 缺点 | |
|---|---|---|
| 方式一:直接对结点按层编号,然后再将各结点按编号存入数组。 | 节省存储空间。 | 无法根据结点间的下标关系确定它们之间的逻辑关系,从而难以实现二叉树求父、子结点等基本运算。 |
| 方式二:先增设虚拟节点,将其转为一棵完全二叉树,然后再按层编号存入数组。 | 方便实现二叉树求父、子结点等基本运算。 | 浪费存储空间。 |
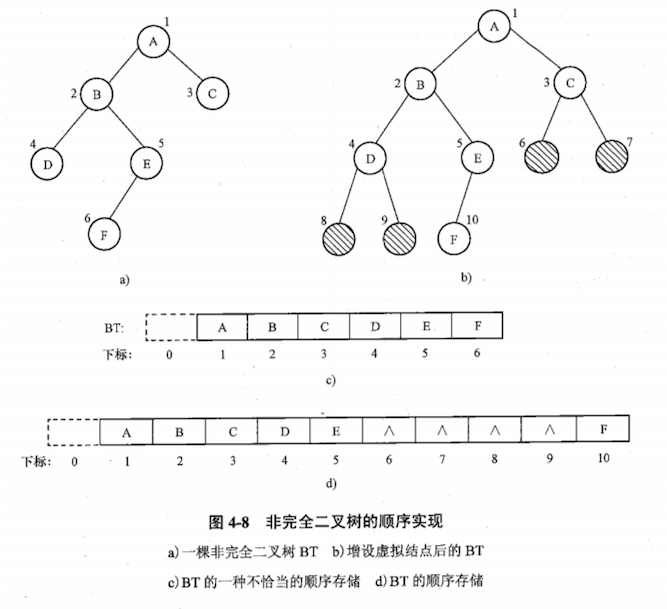
所以,如果某棵二叉树是一棵完全二叉树,那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样,要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因,也是为什么完全二叉树要求最后一层的子节点都靠左的原因。
当我们讲到堆和堆排序的时候,你会发现,堆其实就是一种完全二叉树,最常用的存储方式就是数组。
二叉树有不同的链式存储结构,其中最常用的是二叉链表和三叉链表,其结点形式如下图:

二叉树的两种链式存储结构如下图:
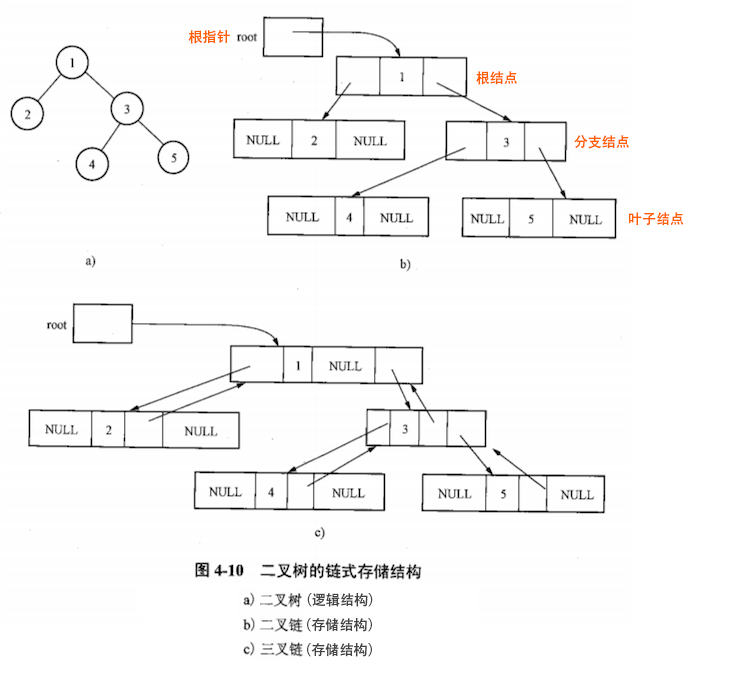
其中,判断叶子结点的条件为:(p->lchild == NULL) && (p->rchild == NULL)。
树常见的基本运算如下:
https://en.wikipedia.org/wiki/Tree_traversal
二叉树的遍历(traversing binary tree),是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问有且仅被访问一次。
二叉树的遍历,有三种经典方式:
| 经典的三种遍历方式 | 遍历顺序 | 推导 |
|---|---|---|
| 先序遍历 | DLR | 首先访问父节点,因此先序序列的第一个结点必为根节点 (如下图先序遍历 A) |
| 中序遍历 | LDR | 先于根结点的为左子树,后于根结点的为右子树 |
| 后序遍历 | LRD | 最后访问父节点,因此后序序列的最后一个结点必为根节点 (如下图后序遍历 A) |
已知二叉树,求三种遍历序列:
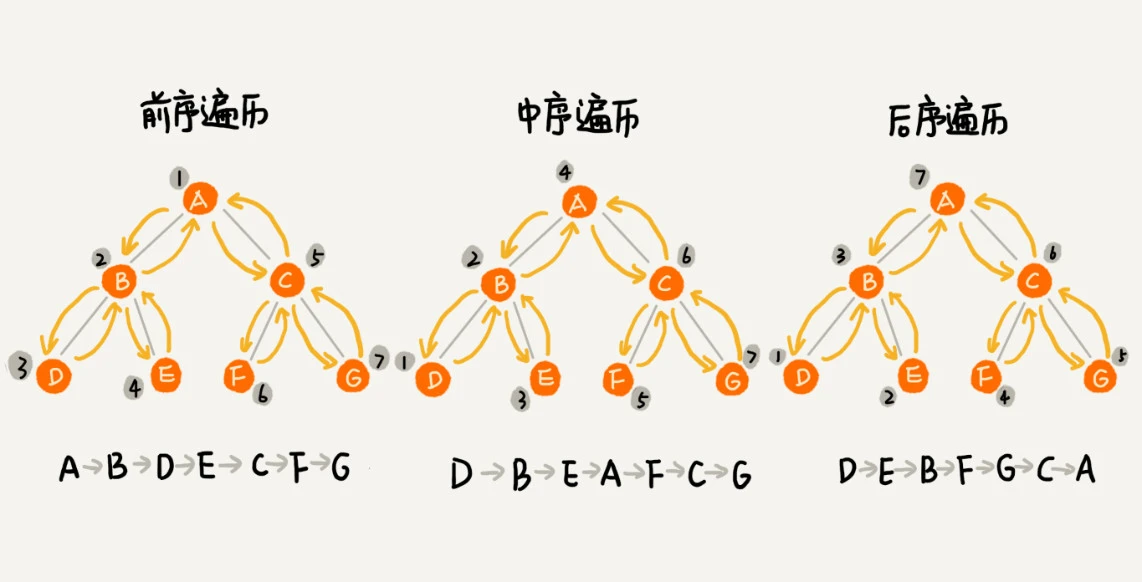
归纳:
由二叉树的遍历可知,任意一棵二叉树结点的先序序列、中序序列和后序序列都是唯一的。已知先序或后序序列 + 中序序列,可以确定一棵二叉树:
问题:
BACDEFGH 和 BCAEDGHF,建立该二叉树。分析:
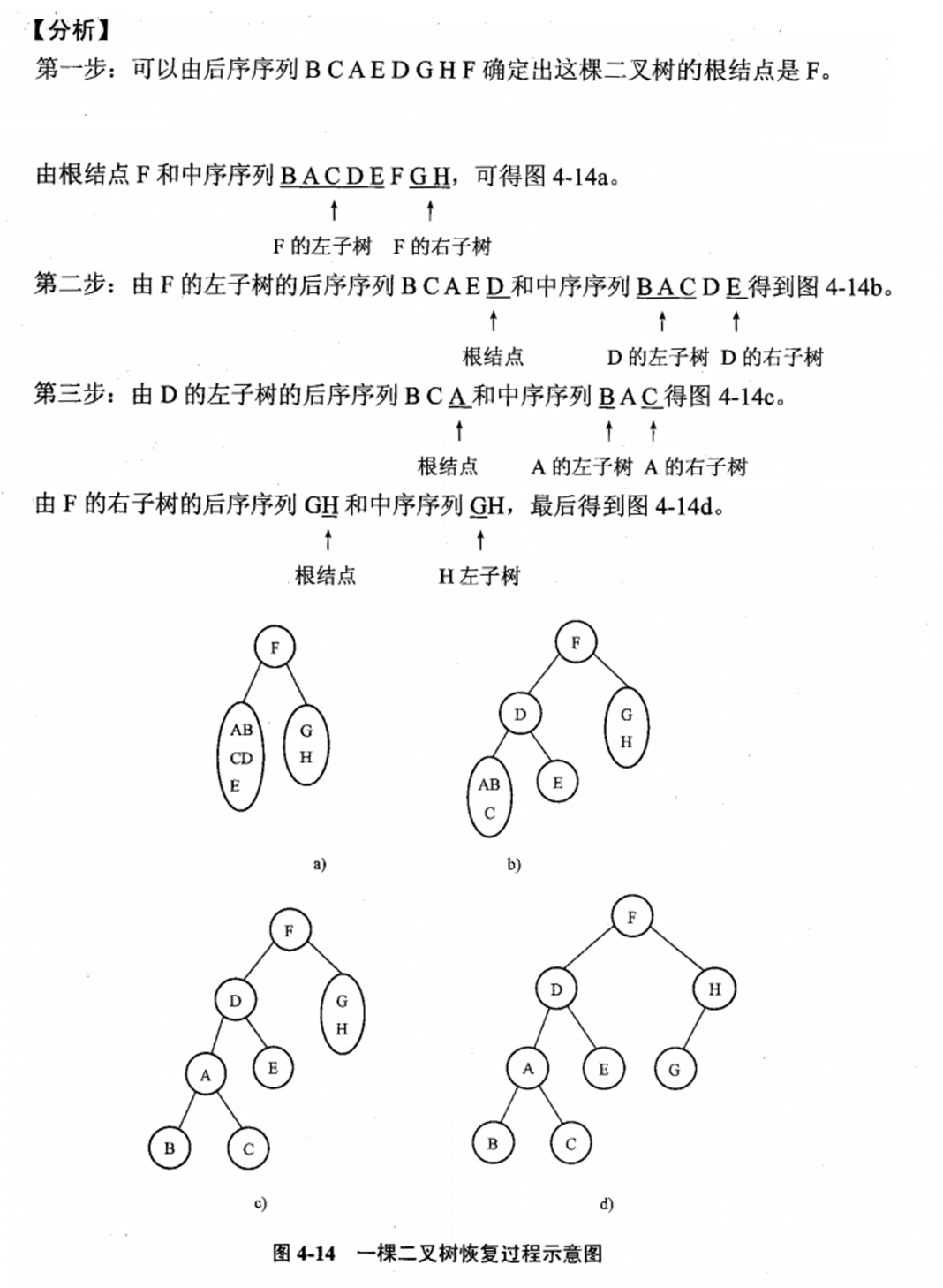
B-tree 的阶(Order),来自 Knuth (1998) 的定义:
Knuth (1998) defining the order to be maximum number of children (which is one more than the maximum number of keys).
所以按照 Knuth 定义一棵 m 阶的 B 树(国内教材所用的定义):
Every node has at most m children.
每个节点最多有 m 个孩子。
Every non-leaf node (except root) has at least ⌈m/2⌉ child nodes.
非叶非根节点至少有 [m/2] 个儿子。[m/2] 表示取大于 m/2 的最小整数。
The root has at least two children if it is not a leaf node.
根节点至少有 2 个儿子。除非它本身是叶子节点,即整棵树只有它一个节点。
A non-leaf node with k children contains k − 1 keys.
非叶节点:有 k 个儿子,就有 k-1 个 keys。
All leaves appear in the same level and carry no information.
所有叶子节点在同一层,不携带信息 data。
例如一棵 3 阶 B 树,高度相比二叉树会更低。
特性:
为什么用?
为了减少内存开销和磁盘 IO
B+树非叶子节点上是不存储数据的,仅存储键值,而B树节点中不仅存储键值,也会存储数据。之所以这么做是因为在数据库中页的大小是固定的,innodb中页的默认大小是16KB。如果不存储数据,那么就可以存储更多的键值,相应的树的阶数就会更大,树就会更矮更胖,如此一来我们查找数据进行磁盘的IO次数会再次减少,数据查询的效率也会更快。另外,B+树的阶数是等于键值的数量的,如果我们的B+树一个节点可以存储1000个键值,那么3层B+树可以存储1000×1000×1000=10亿个数据。一般根节点是常驻内存的,所以一般我们查找10亿数据,只需要2次磁盘IO。
为了支持区间查找
因为B+树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列的,叶子节点间通过双向链表连接。那么B+树使得范围查找,排序查找,分组查找以及去重查找变得异常简单。而B树因为数据分散在各个节点,要实现这一点是很不容易的。
https://en.wikipedia.org/wiki/Tree_structure
无回路的连通图(Connected Graph)即为树。
森林(Forest):n 棵互不相交的树的集合。
A set of n ≥ 0 disjoint trees.
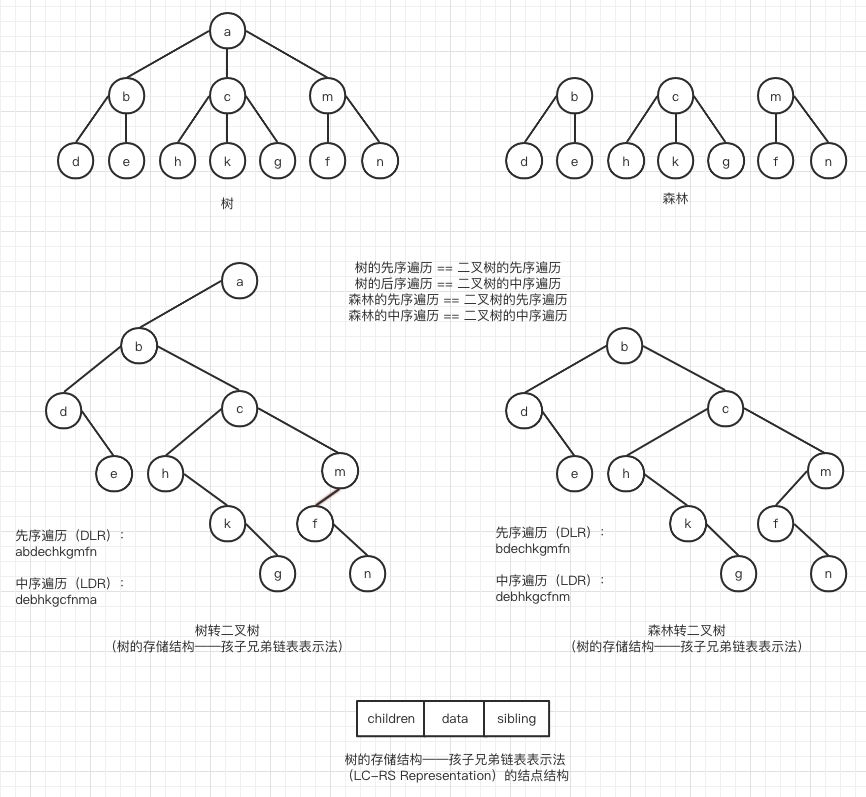
https://blog.csdn.net/chengyq116/article/details/112342319
https://slidetodoc.com/left-childright-sibling-representation-instructor-prof-jyhshing-roger/
https://en.wikipedia.org/wiki/Huffman_tree
哈夫曼树的性质:
【霍夫曼编码原理 文本压缩、ZIP压缩文件原理 Huffman Encoding by Tom Scott-哔哩哔哩】 https://b23.tv/wFatkFc
【Huffman 编码动画演示】 https://www.bilibili.com/video/BV18V411v7px/
中序遍历时从小到大的二叉树。
《29 | 堆的应用:如何快速获取到 Top 10 最热门的搜索关键词?》
B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children.[2]Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as disks. It is commonly used in databases and file systems.
B+ tree can be viewed as a B-tree in which each node contains only keys (not key–value pairs), and to which an additional level is added at the bottom with linked leaves.
The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context — in particular, filesystems. This is primarily because unlike binary search trees, B+ trees have very high fanout (number of pointers to child nodes in a node,[1] typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree.
2–3 tree is a B–tree of order 3.
2–3–4 tree is a B–tree of order 4.
R-tree,R 树是 B 树向多维空间发展的另一种形式
《23 | 二叉树基础(上):什么样的二叉树适合用数组来存储?》
《24 | 二叉树基础(下):有了如此高效的散列表,为什么还需要二叉树?》
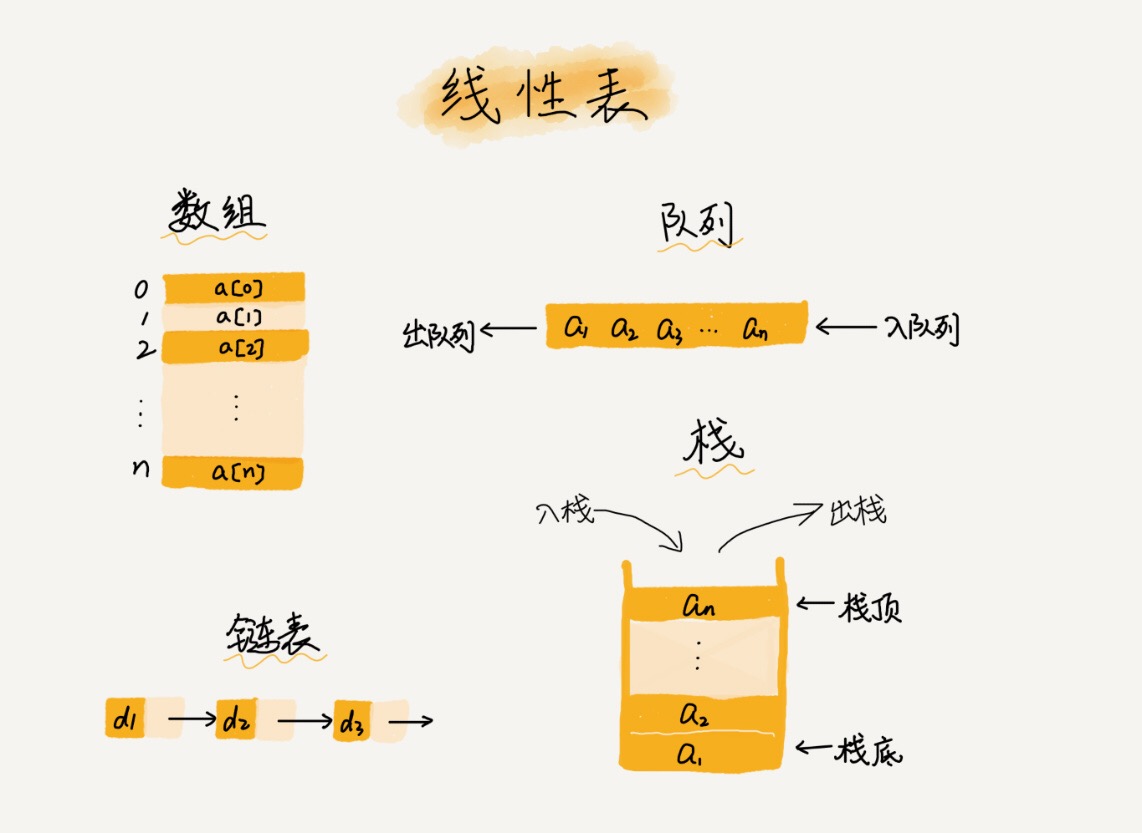
线性表顺序存储的方法是:将表中的结点依次存放在计算机内存中一组连续的存储单元中,数据元素在线性表中的邻按关系决定它们在存储空间中的存储位置,即:逻辑结构中相邻的结点其存储位置也相邻。用顺序存储实现的线性表称为顺序表。一般使用数组来表示顺序表。因此,数组可以看成线性表的一种推广。
一维数组又称向量(Vector),它由一组具有相同类型的数据元素组成,并存储在一组连续的存储单元中。其存储结构如下图:
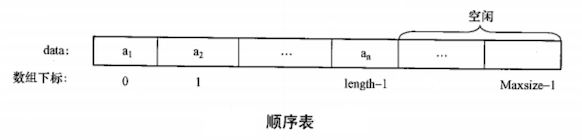
对于可变长数组(Resizable Array)的插入、删除操作,其元素移动情况如下:
| 元素移动次数 (n 为数组大小, i 为操作位置) |
平均移动次数 | 时间复杂度 | |
|---|---|---|---|
| 插入 | $n-i+1$ 次 | $n/2$ 次 | O(n) |
| 删除 | $n-i$ 次 | $(n-1)/2$ 次 | O(n) |
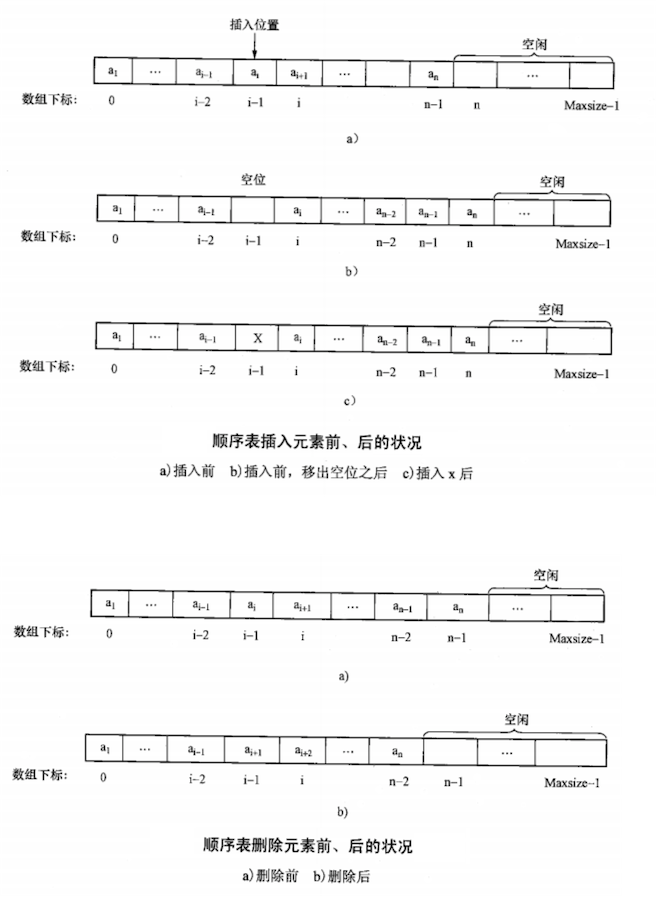
若一维数组中的数据元素又是一维数组结构,则称为二维数组,以此类推。一般地,一个 n 维数组可以看成元素为 n-1 维数组的线性表。
二维数组的地址计算(行优先)如下:
$$
loc[i,\ j]=loc[0,\ 0]+(n*i+j)*k
$$
其中,$i$ 为行坐标,$j$ 为列坐标,$n$ 为总列数,$k$ 为存储单元。
由公式可知,数组元素的存储位置是下标的线性函数。
矩阵(Matrix)是很多科学计算问题研究的对象,矩阵可以用二维数组来表示。
在数值分析中经常出现一些高阶矩阵,这些高阶矩阵中有许多值相同的元素或者零元素,如果值相同的元素或者零元素在矩阵中的分布有一定规律,称此类矩阵为特殊矩阵。矩阵的非零元素个数很少的矩阵称为稀疏矩阵。
为了节省存储空间,对这类矩阵采用多个值相同的元素只分配一个存储空间,零元素不存储的策略,这一方法称为矩阵的压缩存储。
四种链表对比:
| 四种链表 | 非循环 | 循环(Cycle) |
|---|---|---|
| 单向(Singly) | 单向链表 | 单向循环链表 |
| 双向(Doubly) | 双向链表 | 双向循环链表 |
其中,是否循环的关键代码差异如下:
| 关键代码 | 非循环链表 | 循环链表 |
|---|---|---|
| 判断是否空链表 | head->next == NULL |
head->next == head |
| 判断是否尾结点 | p->next == NULL |
p->next == head |
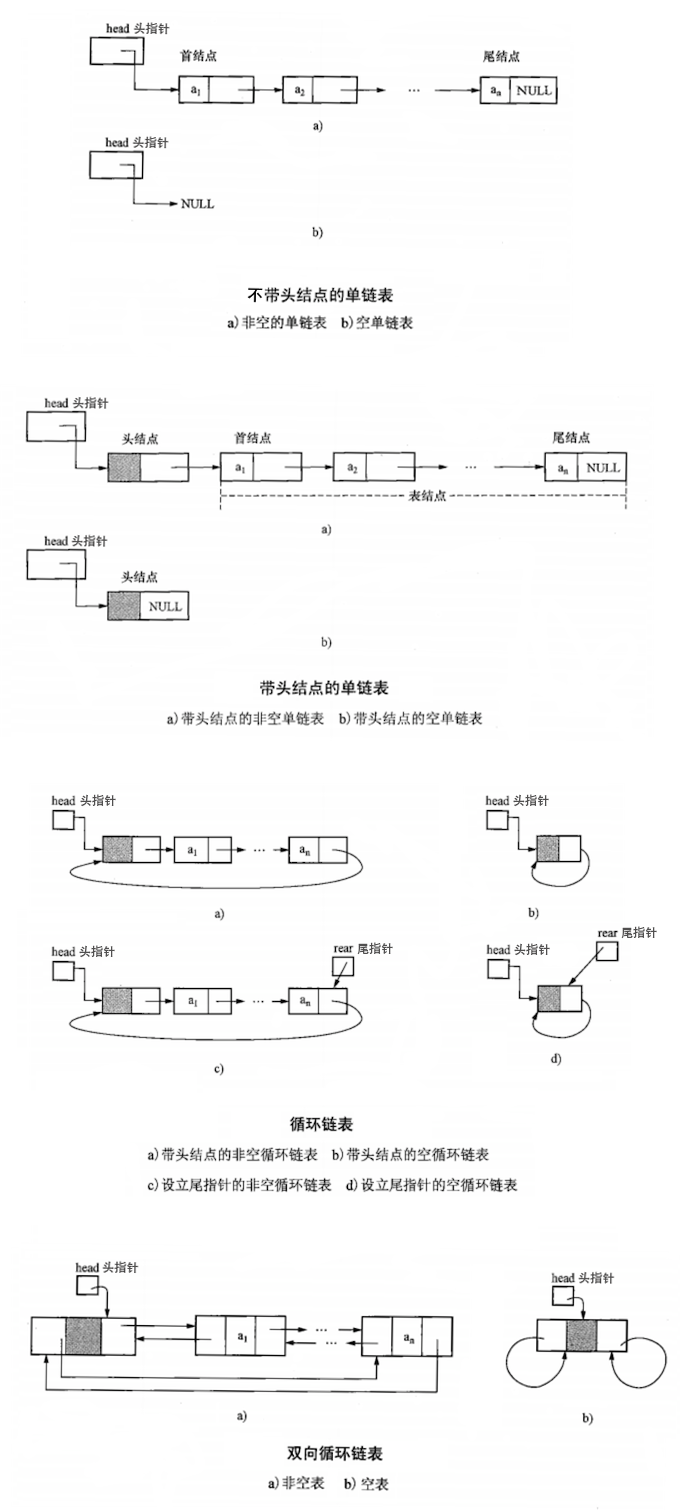
单链表插入(insert p before i)、删除(delete i)结点操作如下:
1 | // 单链表需要先找到 i - 1 结点以便进行插入、删除操作 |
注意:等号左边是指针,等号右边是结点。
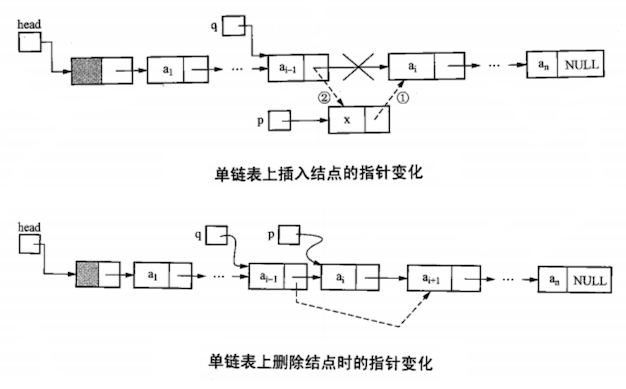
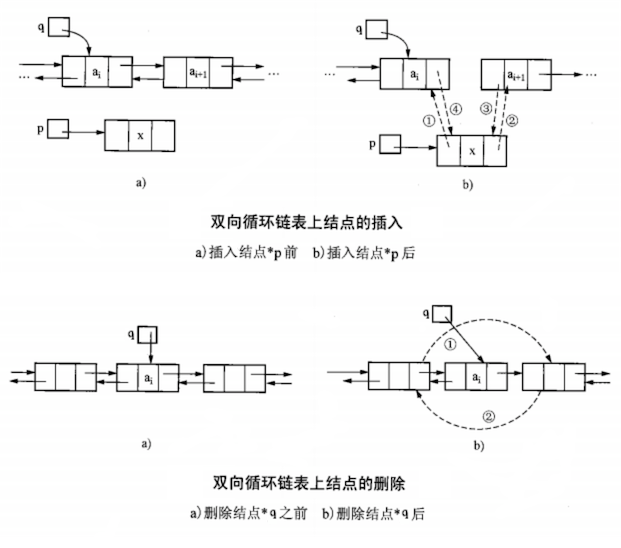
双向循环链表插入(insert p after i)、删除(delete i)结点操作如下:
1 | // 双向循环链表直接获取 i 结点即可,因为可以通过其前驱、后继指针直接进行插入、删除操作 |
注意:等号左边是指针,等号右边是结点
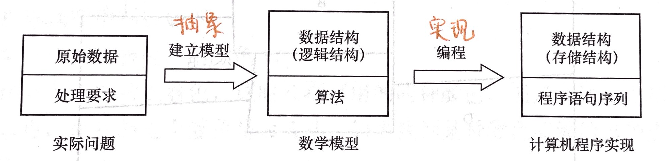
计算机解决一个具体问题时,一般需要经过以下几个步骤:

https://en.wikipedia.org/wiki/Abstract_data_type
任意两个结点之间都没有邻接关系,组织形式松散:
集合的三大特性:
集合之间可以进行运算:
| 数学符号 | 含义 | 英文 |
|---|---|---|
| ∩ | 交 | Intersection |
| ∪ | 并 | Union |
| − | 差 | Difference |
集合的实现:
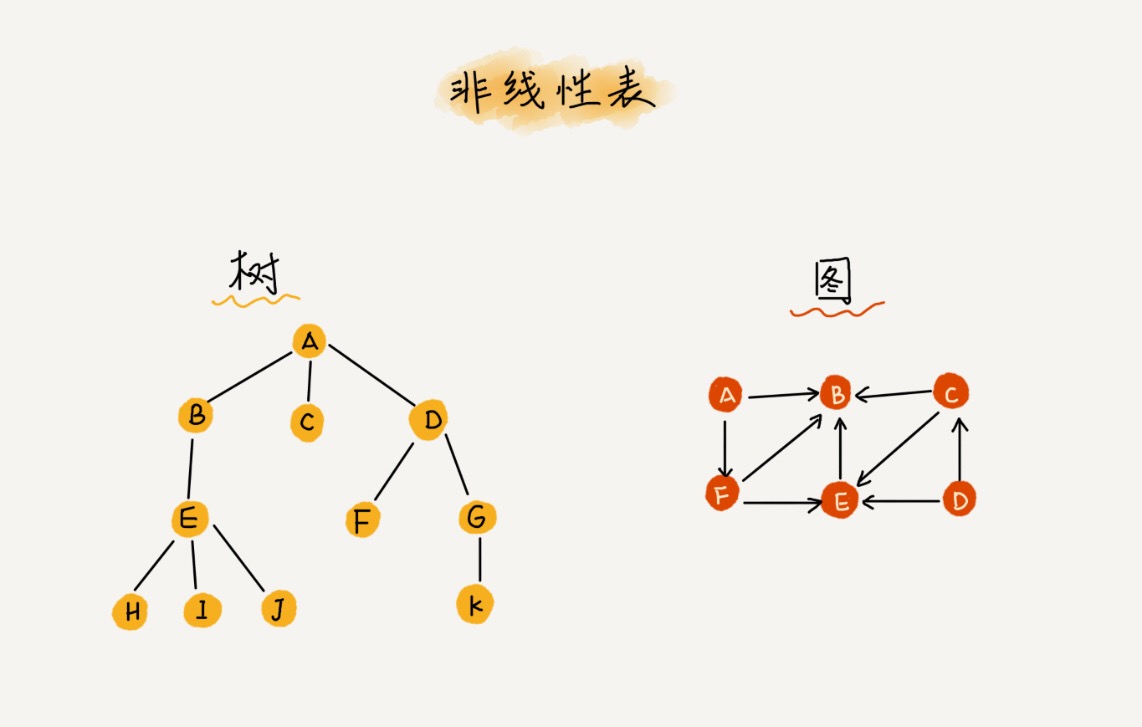
顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
而与它相对立的概念是非线性表,比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,数据之间并不是简单的前后关系。

特征:
父子(1:N)
有没有想过为啥只有二叉树,而没有一叉树?实际上链表就是特殊的树,即一叉树。
地图(N:M)
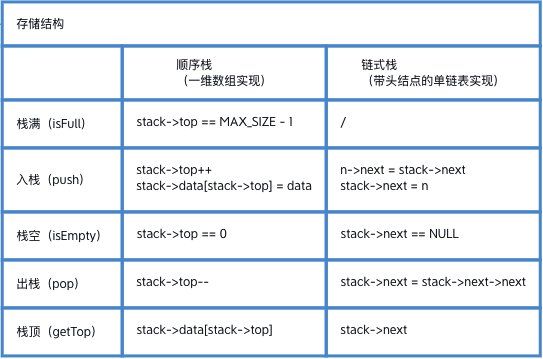
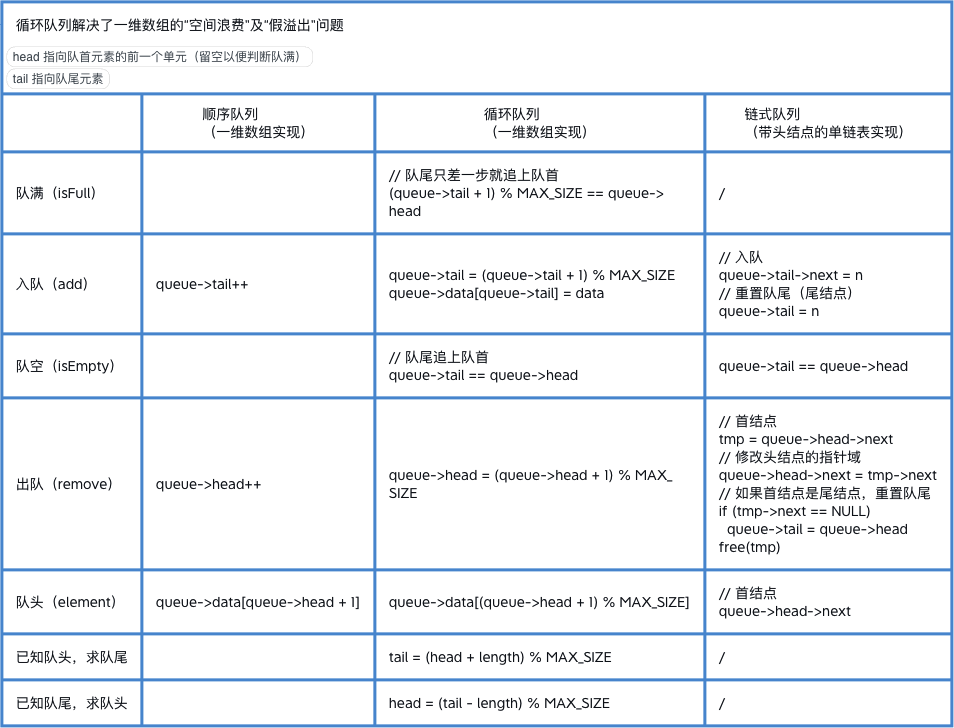
数据的逻辑结构在计算机中的实现,称为数据的存储结构(或物理结构)。
一般情况下,一个存储结构包括以下两个部分:
逻辑结构常见的存储结构实现如下:
| 顺序存储方式 | 链式存储方式 | 散列存储方式 | 索引存储方式 | |
|---|---|---|---|---|
| 集合结构 | 散列表(Hash Table) | |||
| 线性结构 | 数组(一维、二维) 顺序栈 循环队列(取余运算) |
链表(单向/双向、是否循环) 链栈 链队列 |
||
| 树形结构 (二叉树) |
一维数组 |
链表 |
||
| 树形结构 (多叉树) |
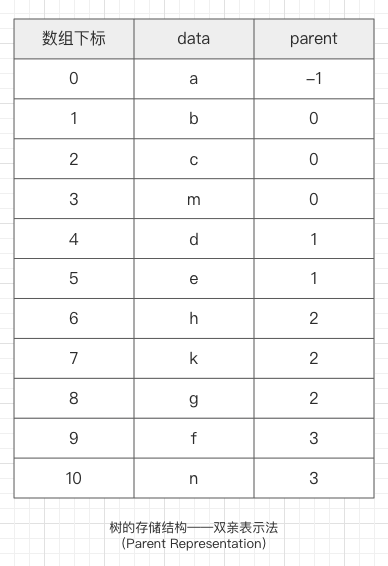
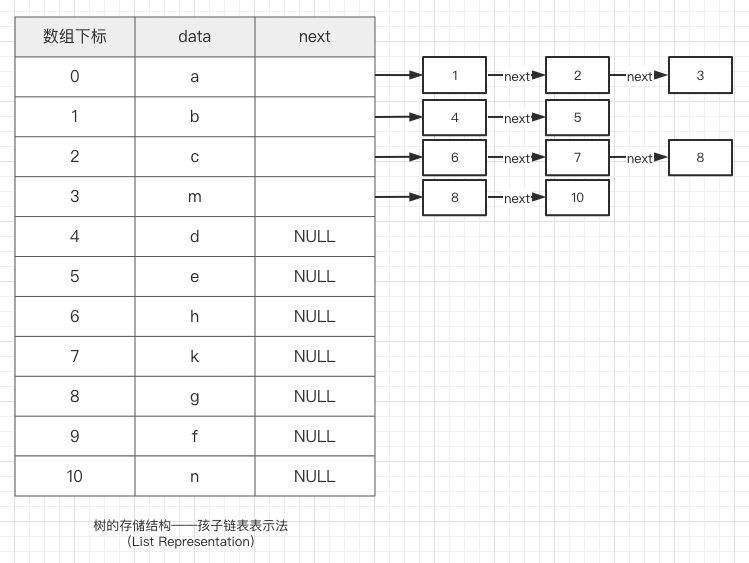
双亲表示法(一维数组) | 孩子链表表示法(一维数组 + 单链表) 孩子兄弟表示法(二叉链表,LC-RS) |
||
| 图结构 | 邻接矩阵(二维数组) | 邻接表(一维数组 + 单链表) |
所有存储结点存放在一个连续的存储区中。利用结点在存储区中的相对位置来表示数据元素之间的逻辑关系。
每个存储结点除了含有一个数据元素之外,还包含指针,每个指针指向一个与本结点有逻辑关系的结点。利用指针表示数据元素之间的逻辑关系。
散列表(Hash Table)。
基本运算,是指在某种逻辑结构上施加的操作,即对逻辑结构的加工。这种加工以数据的逻辑结构为对象。一般而言,在每个逻辑结构上,都定义了一组基本运算,这些运算包括:等。
定义:一个算法规定了求解给定问题所需的处理步骤及其执行顺序,使得给定问题能在有限时间内被求解。
算法分析:

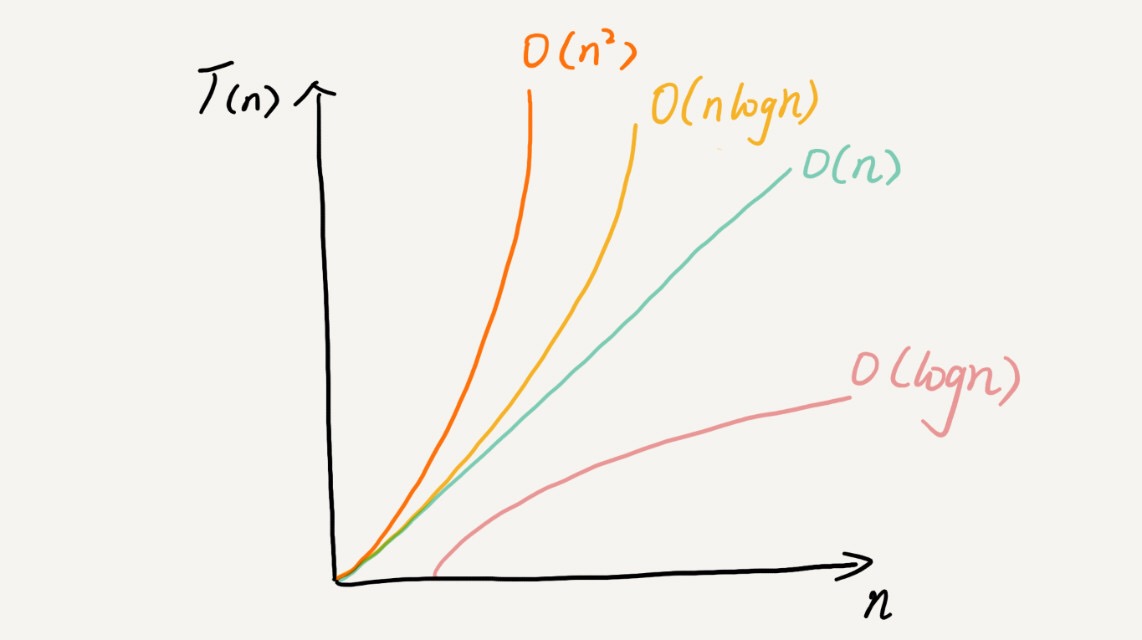
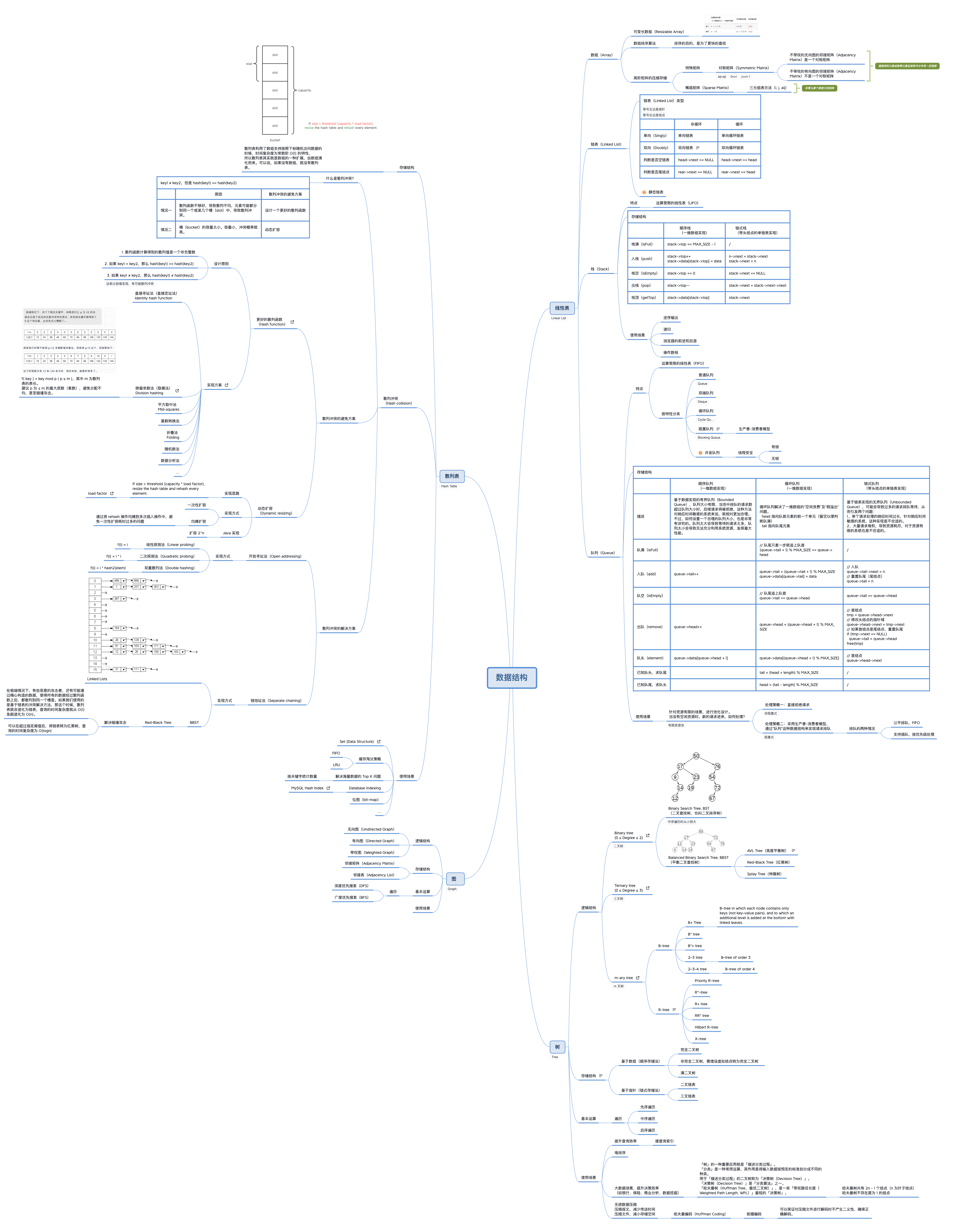
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
参考文档:https://brew.sh/
安装目录:/usr/local/Cellar

常用的 cask:
1 | $ brew install --cask iterm2 |
常用的 formula:
1 | $ brew install coreutils |

https://www.mongodb.com/zh-cn/docs/manual/tutorial/install-mongodb-on-os-x/
https://github.com/mongodb/homebrew-brew
1 | $ brew tap mongodb/brew |

1 | $ brew services start mysql@8.4 |
Homebrew 源替换为 USTC 镜像:http://mirrors.ustc.edu.cn/help/brew.git.html
Homebrew 关闭自动更新:https://github.com/Homebrew/homebrew-autoupdate
1 | export HOMEBREW_NO_AUTO_UPDATE="1" |
原则13:从硬件、操作系统到你使用的编程语言等多方面深入了解服务器的工作原理。优化 IO 操作的效率是一个良好架构的首要任务。
原则15:如果你的设计是基于事件驱动的非阻塞架构,那就不要阻塞线程或者在线程中执行 IO 操作。一旦这样做,系统将慢如蜗牛。
本文主要介绍和对比 socket 常用的几种 I/O 模型:

默认设置下,socket 为同步阻塞 I/O 模型,需阻塞等待新的连接、新的数据报到达:
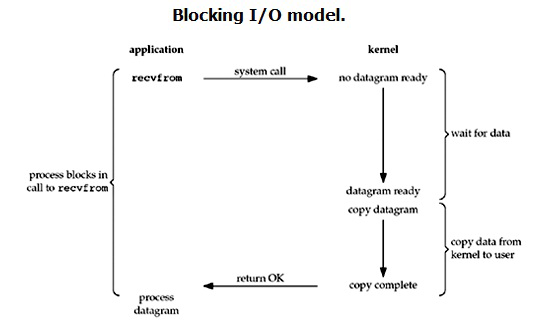
有两种实现方式:
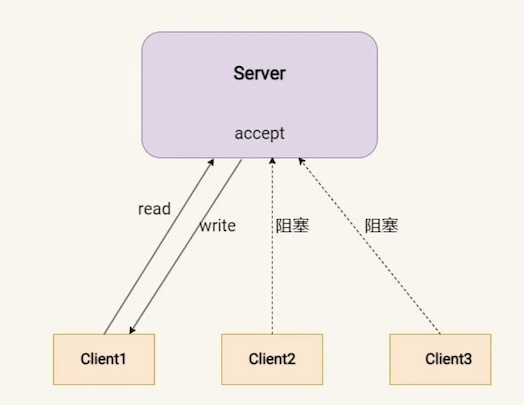
优点:
缺点:
close() 发送 EOF 关闭连接后,才能继续处理 backlog 中的下一个连接。如果该连接一直未关闭,则会阻塞主线程使其一直等待该连接新的数据报到达,导致:
https://github.com/qidawu/cpp-data-structure/blob/main/socket/tcpIterativeServer.c
同步阻塞 I/O + 单线程模型的服务端流程如下:
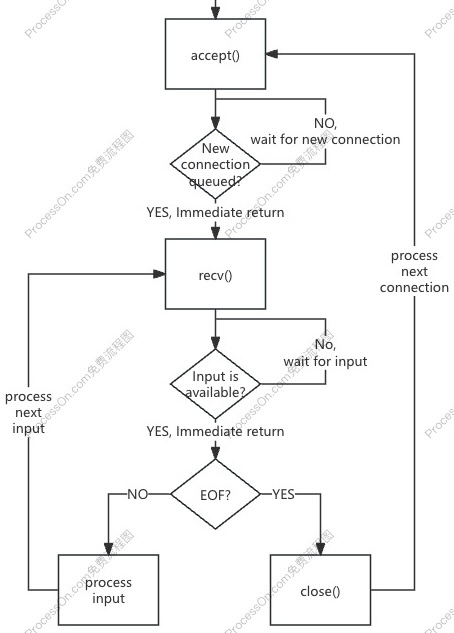
多线程模型(Thread-based architecture / Thread per Request Model)
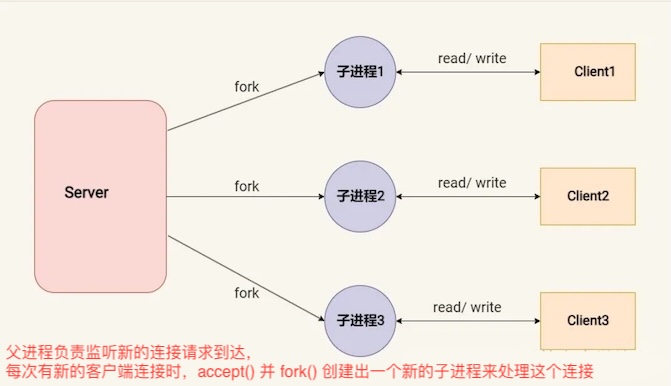
优点:
缺点:
ulimit -u)
有几种设置方式可以将 socket 设置为同步非阻塞 I/O 模型。设置后,需忙轮询(polling)等待新的连接、新的数据报到达:
Then all operations that would block will (usually) return with EAGAIN or EWOULDBLOCK (operation should be retried later); connect(2) will return EINPROGRESS error. The user can then wait for various events via poll(2) or select(2).
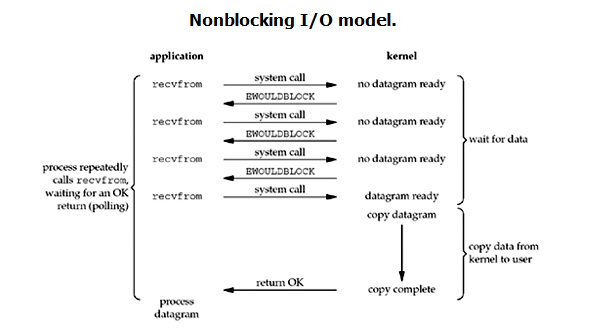
优点:
缺点:
accept()),或者各个已建立的连接是否有新的数据报到达(以便 recv())。反复多次无谓的系统调用,浪费系统资源。同步非阻塞 I/O + 单线程模型的服务端流程如下:
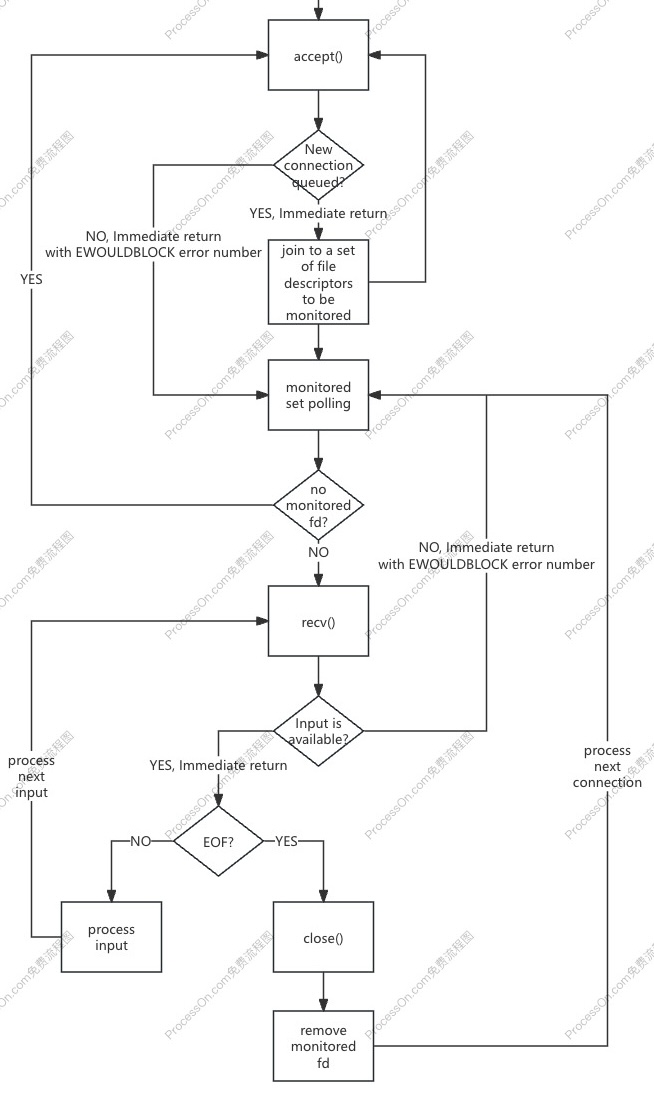
什么是多路复用(Multiplexing)?
In telecommunications and computer networking, multiplexing (sometimes contracted to muxing) is a method by which multiple analog or digital signals are combined into one signal over a shared medium. The aim is to share a scarce resource – a physical transmission medium.
A device that performs the multiplexing is called a multiplexer (MUX), and a device that performs the reverse process is called a demultiplexer (DEMUX or DMX).
In computing, I/O multiplexing can also be used to refer to the concept of processing multiple input/output events from a single event loop, with system calls like poll[1] and select (Unix).[2]
为了减少忙轮询(polling)带来的 CPU 资源消耗,可以使用 I/O 多路复用,同时监视多个文件描述符:
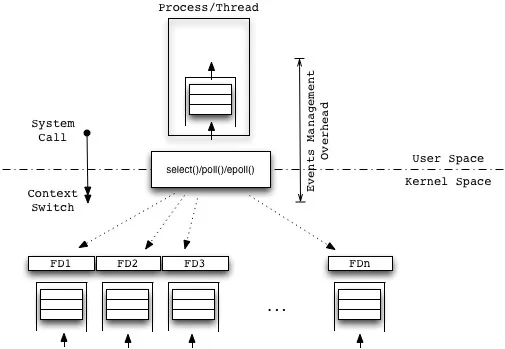
一旦一个或多个文件描述符就绪,就通知程序进行相应的操作:
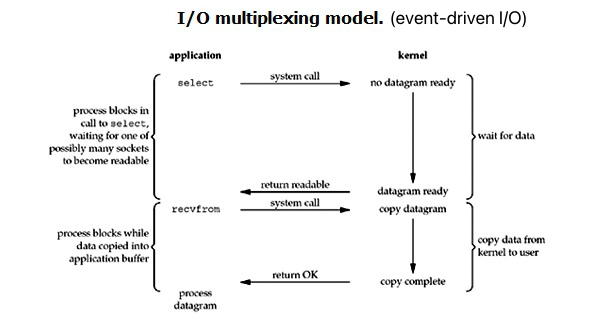
适用场景:
优点:
accept()、recv()),使用 I/O 多路复用只需 1 次系统调用,即可同时监视多个文件描述符是否就绪。I/O 多路复用在各平台的 API 如下:
The classical functions for I/O multiplexing are
selectandpoll. Due to several limitations, modern operating systems provide advanced (non-portable) variants to these:
- Windows provides I/O completion ports (IOCP).
- BSD provides
kqueue.- Linux provides
epoll.- Solaris provides
evport.
I/O 多路复用 API 对比表格:
| 演进 | 诞生时间 | 是否 POSIX 标准 | API 易用程度 | 能够监视的事件 | 能够监视的文件描述符数量 | 性能(用户如何获取已就绪的文件描述符集合) |
|---|---|---|---|---|---|---|
select() |
上世纪 80 年代 | 是 | 低(每次 select() 完都需重置 fd_set) |
readfdswritefdsexceptfds |
< 1024 | 低(轮询实现) |
poll() |
1997 年 | 是 | 中 | POLLINPOLLOUTPOLLPRIPOLLERRPOLLHUPPOLLRDHUP |
≥ 1024 | 低(轮询实现) |
epoll |
2002 年 Linux 2.5.44 | 否 | 高 | EPOLLINEPOLLOUTEPOLLPRIEPOLLERREPOLLHUPEPOLLRDHUP |
≥ 1024 | 高(红黑树+双向链表) |
https://man7.org/linux/man-pages/man2/select.2.html
synchronous I/O multiplexing
SYNOPSIS
2
3
4
5
6
7
8
9
10
11
// return value: n, 0, -1
// On success, number of file descriptors contained in the three returned descriptor sets
// 0 if the timeout expired before any file descriptors became ready.
// On error, -1 is returned, and errno is set to indicate the error
int select(int nfds,
fd_set *readfds,
fd_set *writefds,
fd_set *exceptfds,
struct timeval *timeout);DESCRIPTION
⚠️WARNING:
select()can monitor only file descriptors numbers that are less thanFD_SETSIZE(1024)—an unreasonably low limit for many modern applications—and this limitation will not change. All modern applications should instead usepoll(2)orepoll(7), which do not suffer this limitation.
select()allows a program to monitor multiple file descriptors, waiting until one or more of the file descriptors become “ready” for some class of I/O operation (e.g., input possible). A file descriptor is considered ready if it is possible to perform a corresponding I/O operation (e.g.,read(2), or a sufficiently smallwrite(2)) without blocking.
Four macros are provided to manipulate the sets
2
3
4
5
6
7
8
void FD_ZERO(fd_set *set);
// add a given file descriptor from a set
void FD_SET(int fd, fd_set *set);
// remove a given file descriptor from a set
void FD_CLR(int fd, fd_set *set);
// tests to see if a file descriptor is part of the set
int FD_ISSET(int fd, fd_set *set);this is useful after
select()returns.
样例代码参考:
https://man7.org/linux/man-pages/man2/select.2.html#EXAMPLES
<Example: Nonblocking I/O and select() | IBM>
服务端流程如下:
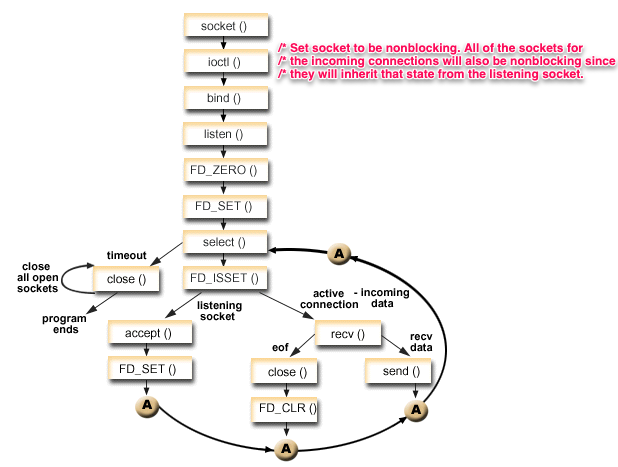
https://man7.org/linux/man-pages/man2/poll.2.html#EXAMPLES
wait for some event on a file descriptor
SYNOPSIS
2
3
int poll(struct pollfd *fds, nfds_t nfds, int timeout);DESCRIPTION
poll()performs a similar task toselect(2): it waits for one of a set of file descriptors to become ready to perform I/O. The Linux-specificepoll(7)API performs a similar task, but offers features beyond those found inpoll().
样例代码参考:
https://man7.org/linux/man-pages/man2/poll.2.html#EXAMPLES
<Using poll() instead of select() | IBM>
https://man7.org/linux/man-pages/man7/epoll.7.html
/proc/sys/fs/epoll/max_user_watches(since Linux 2.6.28)This specifies a limit on the total number of file descriptors that a user can register across all epoll instances on the system.
https://man7.org/linux/man-pages/man2/epoll_create.2.html
open an epoll file descriptor
2
3
4
5
6
// On success, return a file descriptor (a nonnegative integer).
// On error, returns -1 and errno is set to indicate the error.
int epoll_create(int size);
int epoll_create1(int flags);
用法如下:creates a new epoll instance and returns a file descriptor referring to that instance.
1 | int epfd = epoll_create1(0); |
https://man7.org/linux/man-pages/man2/epoll_ctl.2.html
control interface for an epoll file descriptor
2
3
4
5
// On success, returns 0.
// On error, returns -1 and errno is set to indicate the error.
int epoll_ctl(int epfd, int op, int fd, struct epoll_event *event);
op参数支持三种操作:
op Description EPOLL_CTL_ADD增加被监视的文件描述符 EPOLL_CTL_DEL删除被监视的文件描述符 EPOLL_CTL_MOD修改被监视的文件描述符
event参数(结构参考:struct epoll_event)用于描述文件描述符fd。event参数的events成员变量包含两部分含义:event types 和 input flags常用的 event types:
Event types Description EPOLLINThe associated file is available for read(2)operations.EPOLLOUTThe associated file is available for write(2)operations.EPOLLERRError condition happened on the associated file descriptor. This event is also reported for the write end of a pipe when the read end has been closed.
epoll_wait(2) will always report for this event; it is not necessary to set it ineventswhen callingepoll_ctl().EPOLLHUPHang up happened on the associated file descriptor.
epoll_wait(2) will always wait for this event; it is not necessary to set it ineventswhen callingepoll_ctl().常用的 input flags:
Input flags Description EPOLLETRequests edge-triggered notification for the associated file descriptor. The default behavior for epoll is level-triggered. See epoll(7) for more detailed information about edge-triggered and level-triggered notification.
用法如下:adds items to the interest list of the epoll instance
1 | struct epoll_event event; |
https://man7.org/linux/man-pages/man2/epoll_wait.2.html
wait for an I/O event on an epoll file descriptor
2
3
4
5
6
7
// return value: n, 0, -1
// On success, returns the number of file descriptors ready for the requested I/O operation,
// or 0 if no file descriptor became ready during the requested timeout milliseconds.
// On error, returns -1 and errno is set to indicate the error.
int epoll_wait(int epfd, struct epoll_event *events, int maxevents, int timeout);The buffer pointed to by
eventsis used to return information from the ready list about file descriptors in the interest list that have some events available.A call to
epoll_wait()will block until either:
- a file descriptor delivers an event;
- the call is interrupted by a signal handler; or
- the timeout expires.
用法如下:fetchs items from the ready list of the epoll instance
1 | struct epoll_event events[MAXEVENTS]; |
样例代码参考:《如何使用 epoll? 一个 C 语言实例》
epoll 实例由两部分组成:
epoll_ctl() 增删改,数据结构为红黑树。epoll_wait() 返回,数据结构为双向链表。The central concept of the
epollAPI is theepollinstance, an in-kernel data structure which, from a user-space perspective, can be considered as a container for two lists:
- The interest list (sometimes also called the
epollset): the set of file descriptors that the process has registered an interest in monitoring.- The ready list: the set of file descriptors that are “ready” for I/O. The ready list is a subset of (or, more precisely, a set of references to) the file descriptors in the interest list. The ready list is dynamically populated by the kernel as a result of I/O activity on those file descriptors.
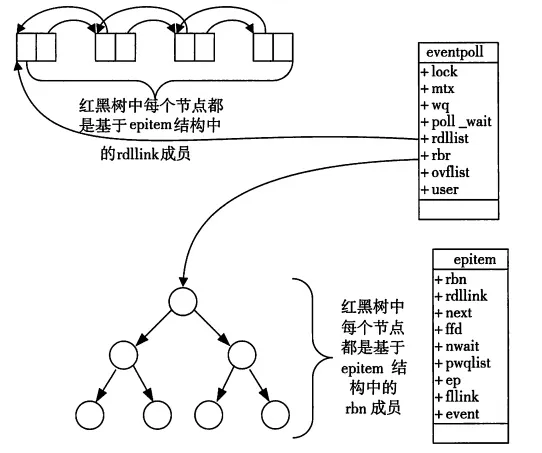
epoll 这种设计能显著提高程序在大量并发连接中只有少量活跃的情况下的系统 CPU 利用率(CPU utilization),因为在 epoll_wait() 获取事件的时候,它无须遍历整个被监视的文件描述符集合(The interest list),只要遍历那些被内核 I/O 事件异步唤醒而加入 Ready 队列的文件描述符集合(The ready list)即可。
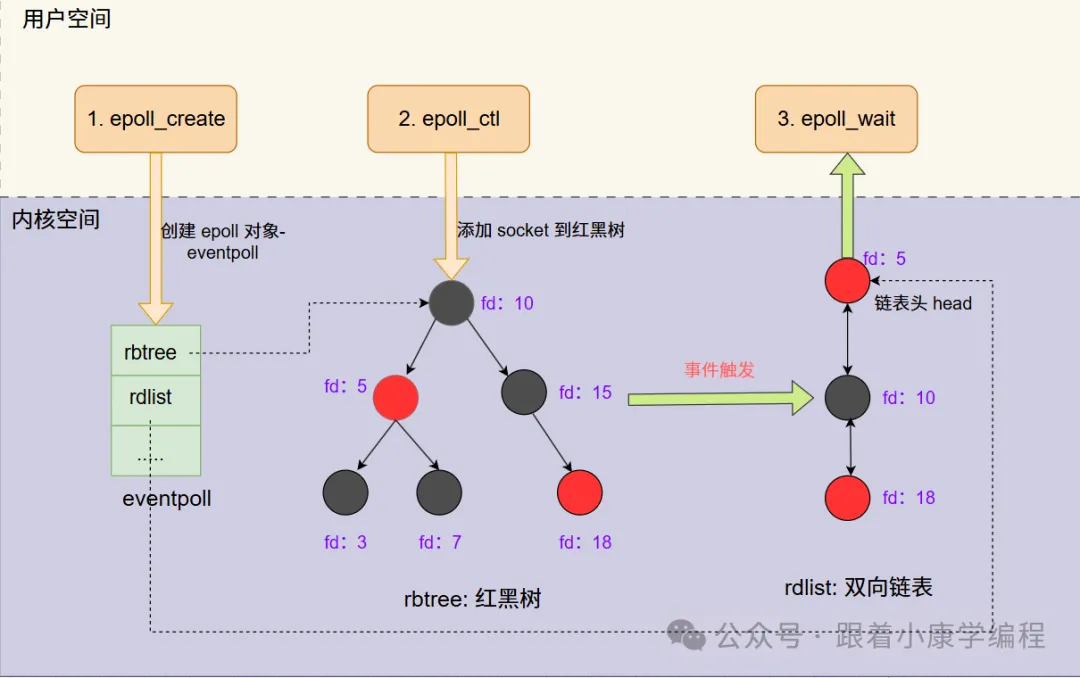
服务端流程如下:
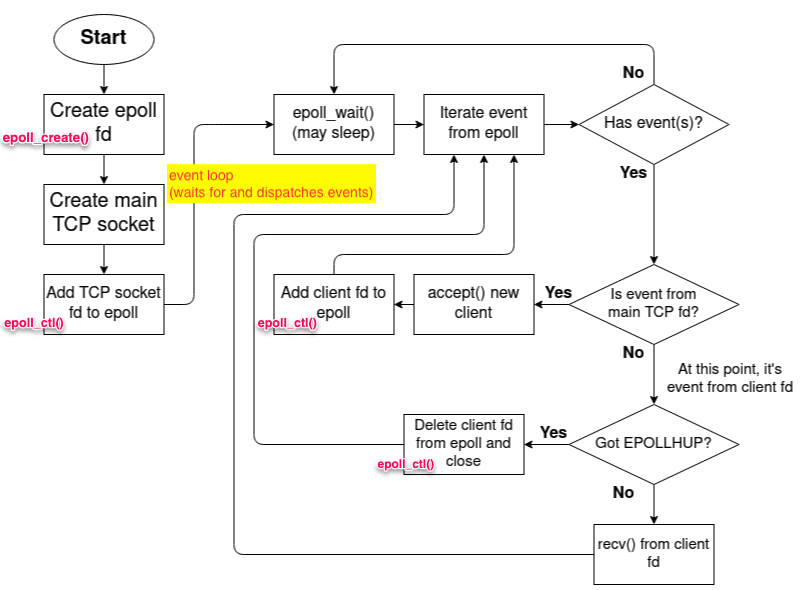
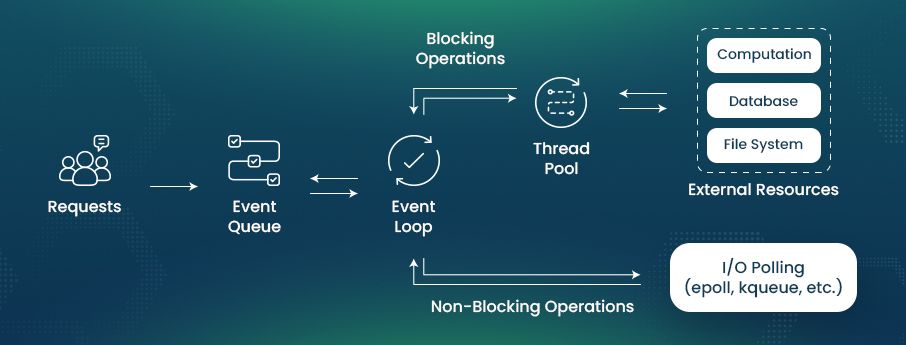
抽象来看,使用 I/O 多路复用可以实现基于单线程的事件循环模型(Single Threaded Event Loop Model):
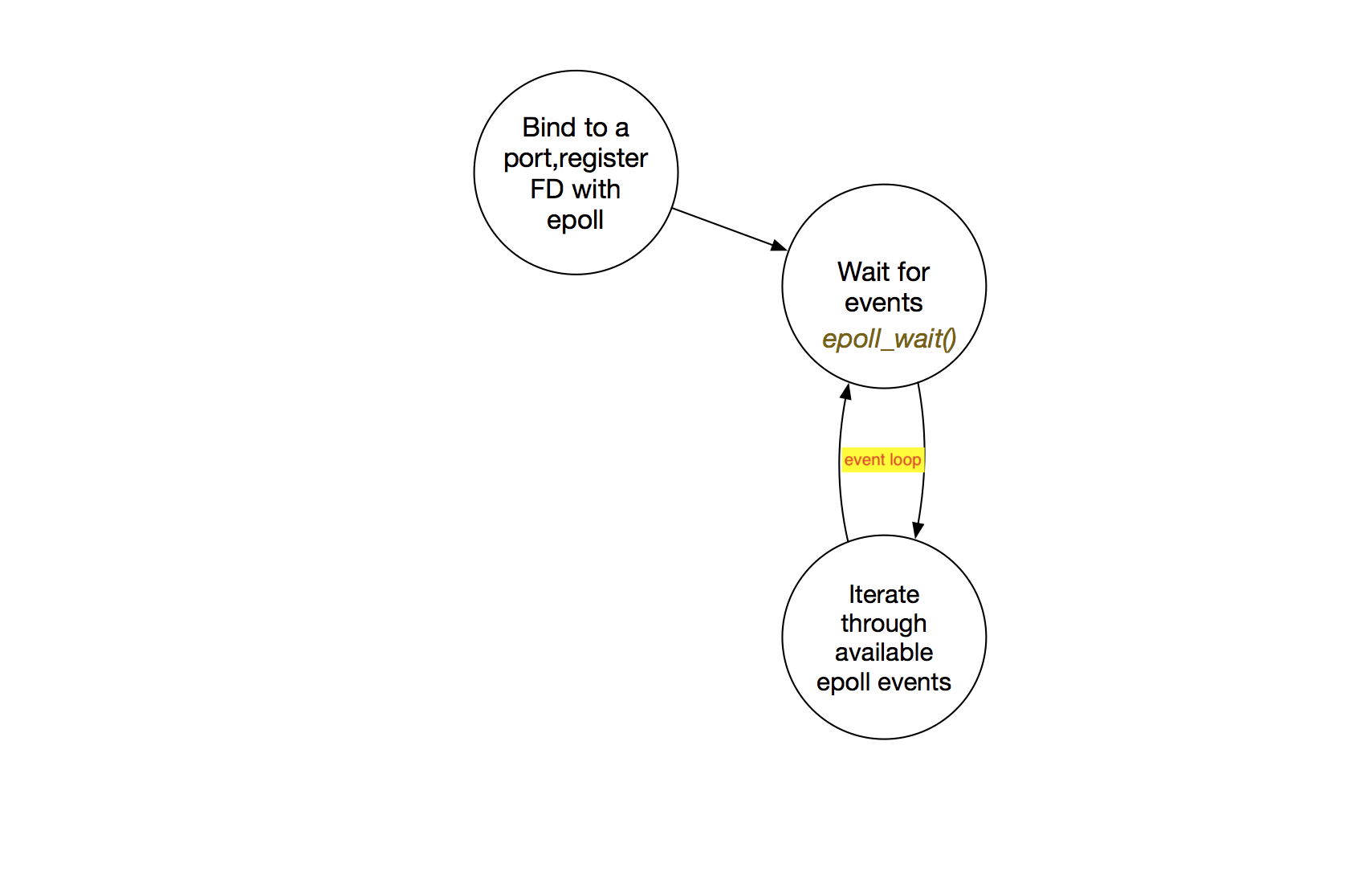
站在客户端、服务端的角度,整体交互流程如下:
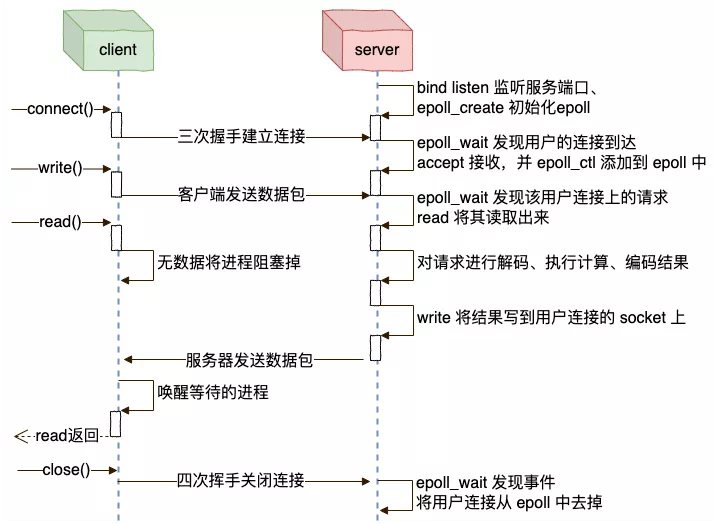
Netty
Redis、Nginx、Node.js、…
通过命令 strace 可以查看应用程序使用了哪些系统调用。例如查看 Redis server 如何使用 epoll API:
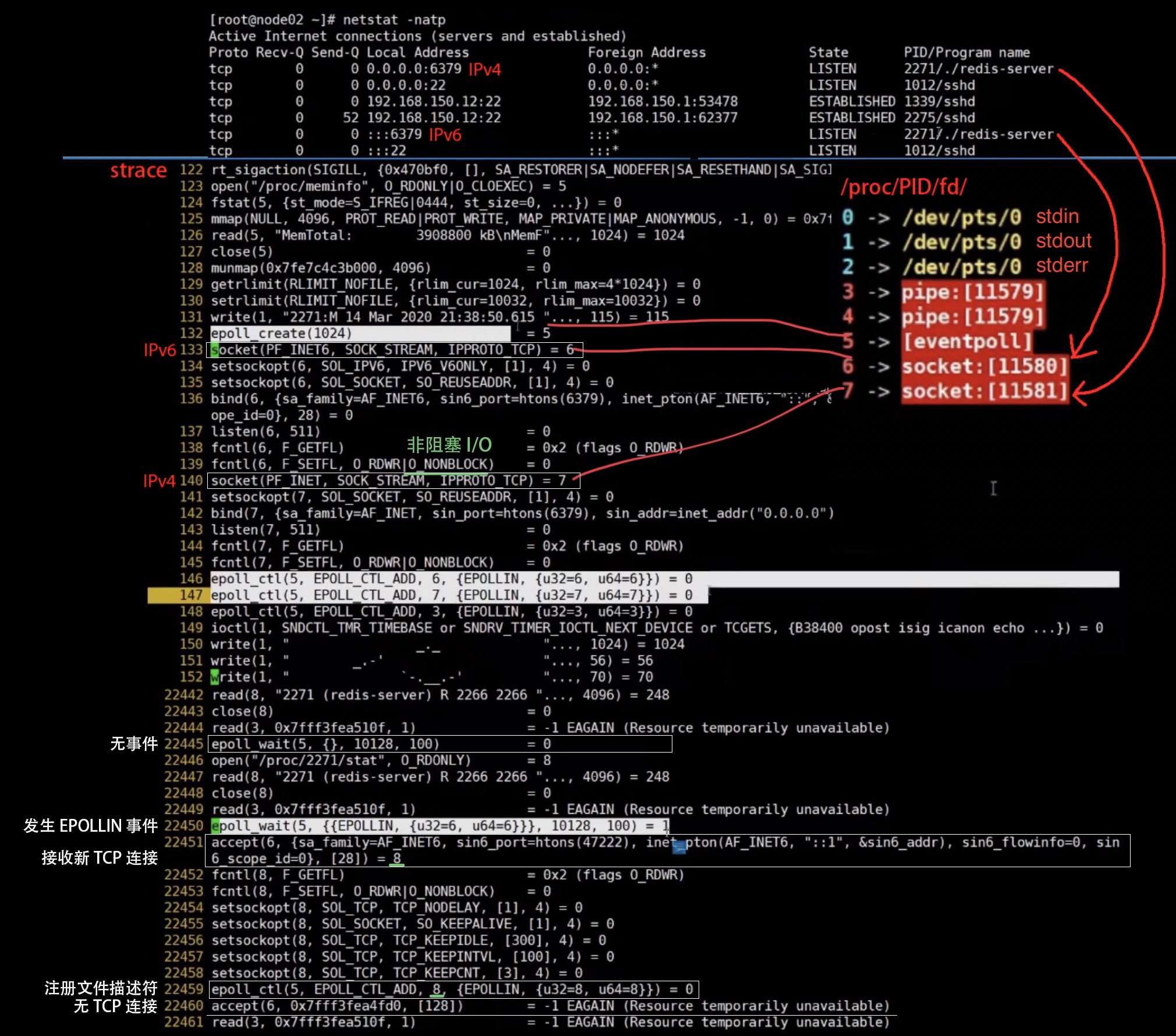
I/O multiplexing
Event loop
Reactor
http://www.kegel.com/c10k.html
I/O 多路复用系列
《Linux 高性能服务 epoll 的本质,真的不简单 | 良许 Linux》
《从 Linux 源码角度看 epoll,透过现象看本质 | 良许 Linux》
《Netty 权威指南》李林峰
参考 Berkeley套接字
Berkeley sockets 也称为 BSD Socket 。伯克利套接字的应用编程接口(API)是采用 C 语言的进程间通信的库,经常用在计算机网络间的通信。 BSD Socket 的应用编程接口已经是网络套接字的事实上的抽象标准。大多数其他程序语言使用一种相似的编程接口。
BSD Socket 作为一种 API,允许不同主机或者同一个计算机上的不同进程之间的通信。它支持多种 I/O 设备和驱动,但是具体的实现是依赖操作系统的。这种接口对于 TCP/IP 是必不可少的,所以是互联网的基础技术之一。它最初是由加州伯克利大学为 Unix 系统开发出来的。所有现代的操作系统都实现了伯克利套接字接口,因为它已经是连接互联网的标准接口了。

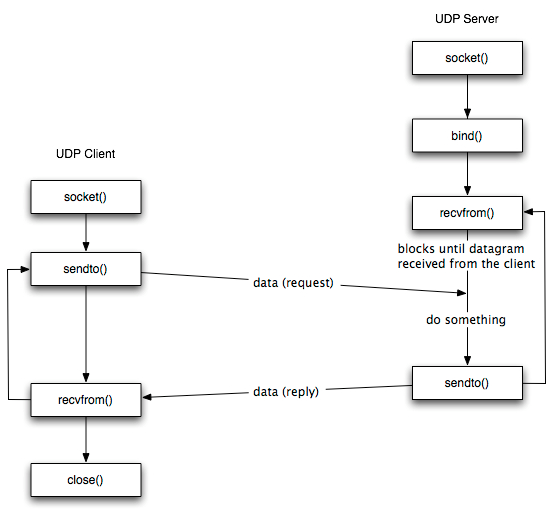
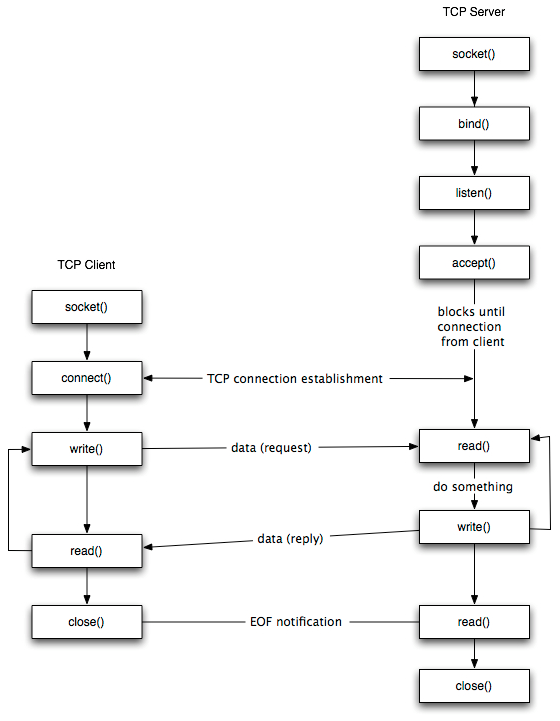
TCP 连接管理(三次握手、四次挥手)的流程及状态机如下:
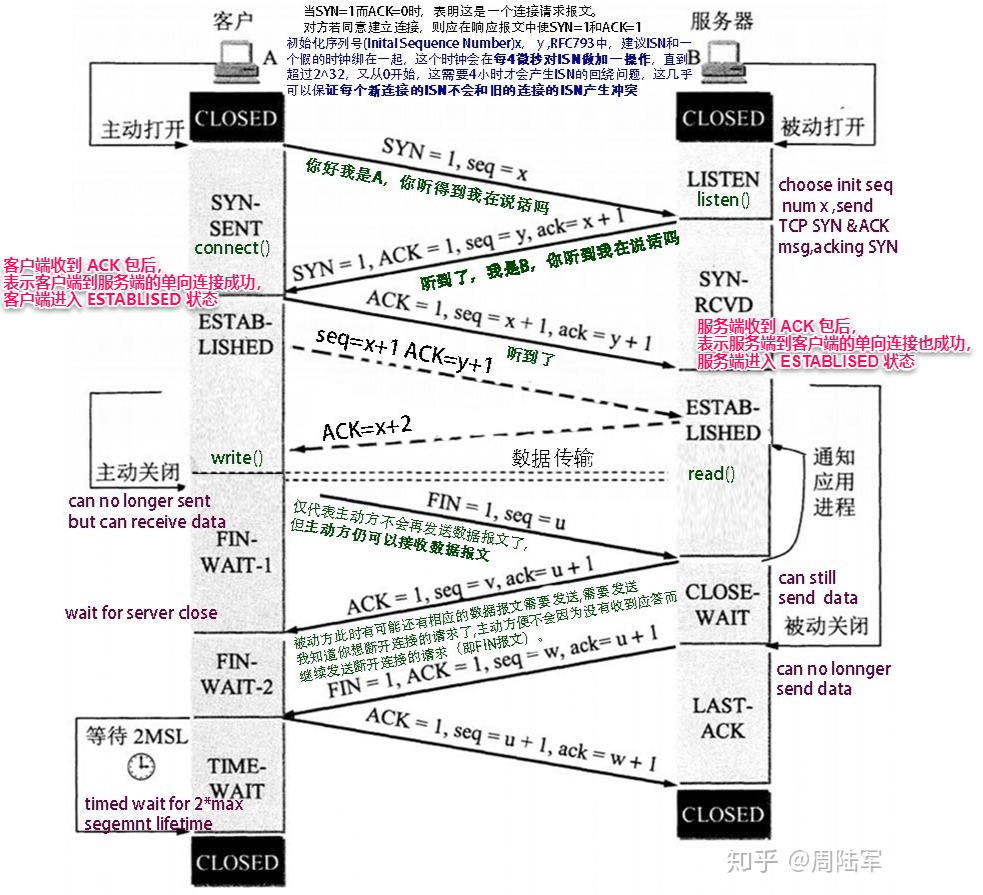
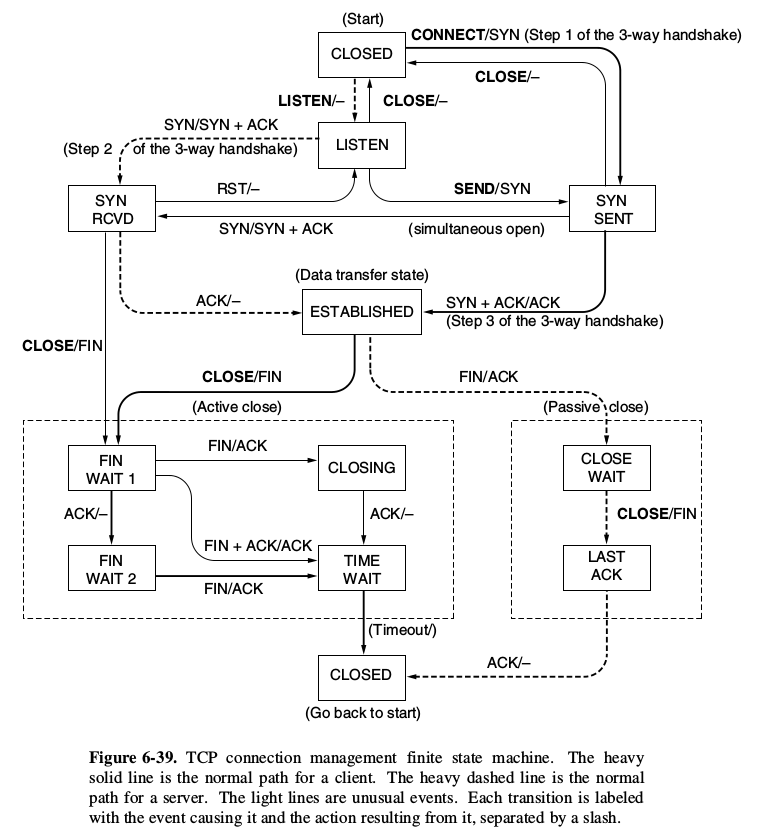
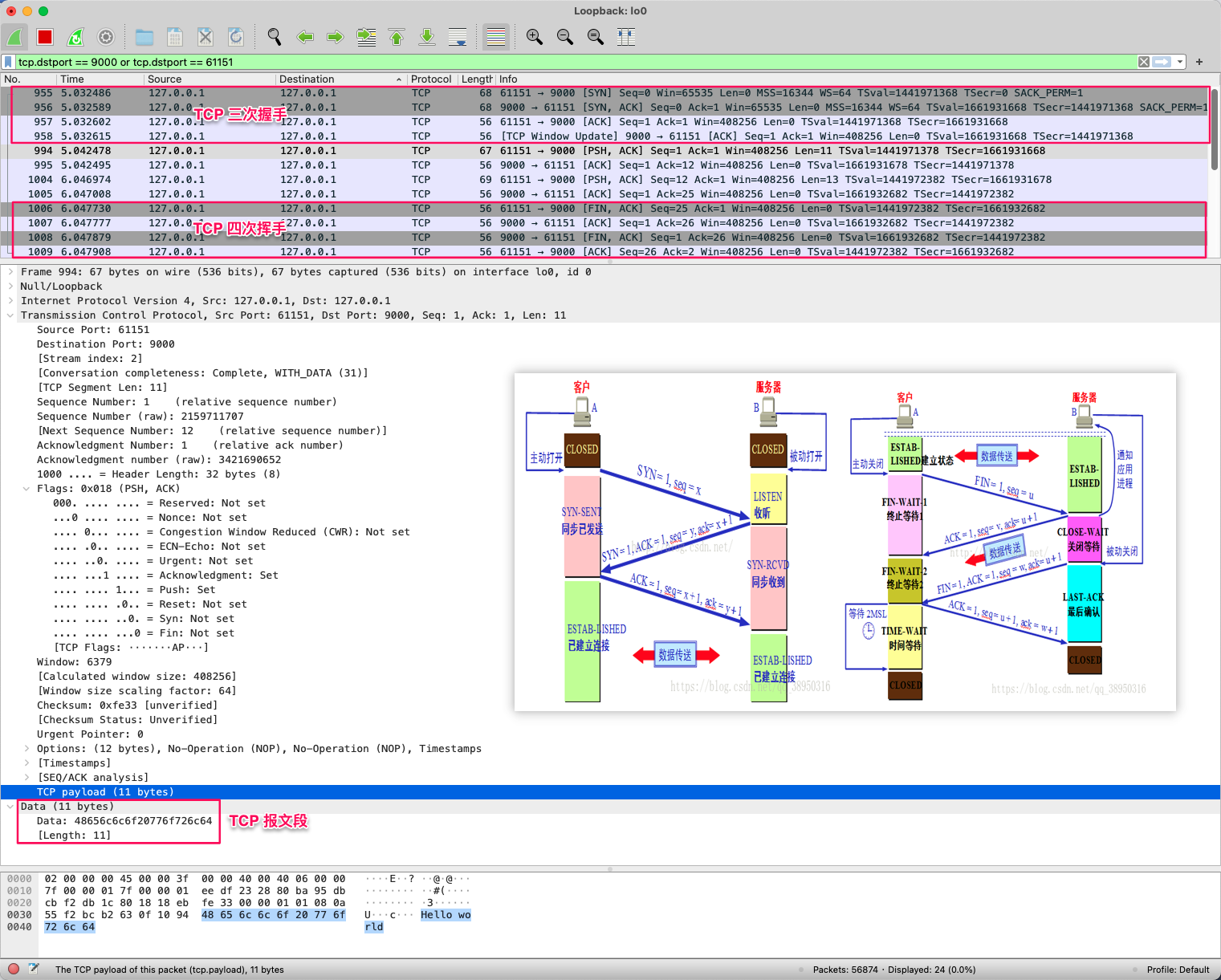
通过 Wireshark 抓包演示如下:在客户端 61151 向服务端 9000 发送两个报文的整个过程,发送之前须三次握手建立连接,发送完毕须四次挥手拆除连接:
https://man7.org/linux/man-pages/man7/socket.7.html
| Syscall | Description | Blocking or not |
|---|---|---|
socket() |
creates an endpoint for communication and returns a file descriptor | NO |
bind() |
bind a name to a socket | NO |
listen() |
listen for connections on a socket | NO |
accept()accept4() |
creates a new file descriptor for an incoming connection | YES or NO (EAGAIN or EWOULDBLOCK) |
connect() |
initiate a connection on a socket | YES or NO (EINPROGRESS) |
recv()send() |
operations on a single file descriptor | YES or NO (EAGAIN or EWOULDBLOCK) |
https://man7.org/linux/man-pages/man2/socket.2.html
SYNOPSIS
2
3
4
5
6
7
// On success, a file descriptor for the new socket is returned.
// On error, -1 is returned, and errno is set appropriately.
int socket(int domain,
int type,
int protocol);DESCRIPTION
socket()creates an endpoint for communication and returns a file descriptor that refers to that endpoint.
domain 参数常用选项:
| Name | Purpose | Man page |
|---|---|---|
AF_INET |
IPv4 Internet protocols | ip(7) |
AF_INET6 |
IPv6 Internet protocols | ipv6(7) |
type 参数常用选项:
SOCK_DGRAM 数据报套接字:Supports datagrams (connectionless, unreliable messages of a fixed maximum length).SOCK_STREAM 流式套接字:Provides sequenced, reliable, two-way, connection-based byte streams. An out-of-band data transmission mechanism may be supported.SOCK_RAW 原始套接字:Provides raw network protocol access.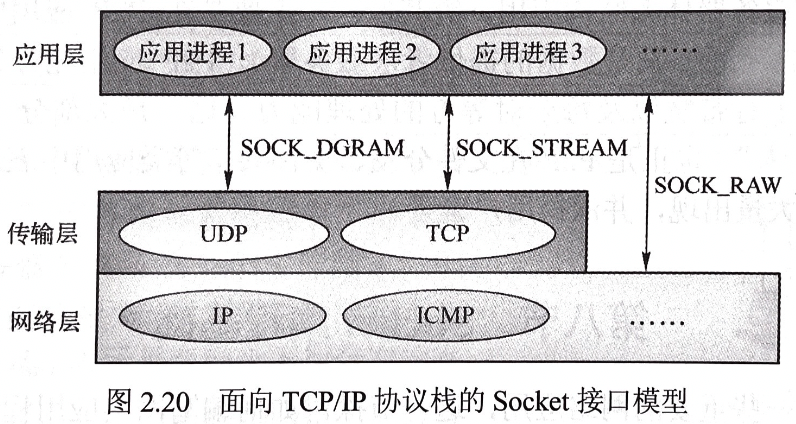
https://man7.org/linux/man-pages/man2/bind.2.html
SYNOPSIS
2
3
4
5
6
7
// On success, 0 is returned.
// On error, -1 is returned, and errno is set appropriately.
int bind(int sockfd,
const struct sockaddr *addr,
socklen_t addrlen);DESCRIPTION
The
bind()assigns a local protocol address to a socket. With the Internet protocols, the address is the combination of an IPv4 or IPv6 address (32-bit or 128-bit) address along with a 16 bit TCP port number.
一般情况下,只有服务端 socket 需要指定端口号。而客户端 socket 为了避免发生端口号冲突,会由操作系统提供的随机临时端口号来运行,用户无须关心。但在某些情况下:
在这种情况下,我们需要显式或强制地使用 bind() 来为客户端 socket 指定特定端口号。
参考:Explicitly assigning port number to client in Socket
https://man7.org/linux/man-pages/man2/listen.2.html
SYNOPSIS
2
3
4
5
6
// On success, 0 is returned.
// On error, -1 is returned, and errno is set appropriately.
int listen(int sockfd,
int backlog);DESCRIPTION
listen()marks the socket referred to by sockfd as a passive socket, that is, as a socket that will be used to accept incoming connection requests usingaccept().The backlog argument defines the maximum length to which the queue of pending connections for sockfd may grow. If a connection request arrives when the queue is full, the client may receive an error with an indication of ECONNREFUSED or, if the underlying protocol supports retransmission, the request may be ignored so that a later reattempt at connection succeeds.
The behavior of the backlog argument on TCP sockets changed with Linux 2.2. Now it specifies the queue length for completely established sockets waiting to be accepted, instead of the number of incomplete connection requests. The maximum length of the queue for incomplete sockets can be set using /proc/sys/net/ipv4/tcp_max_syn_backlog. When syncookies are enabled there is no logical maximum length and this setting is ignored. See tcp(7) for more information.
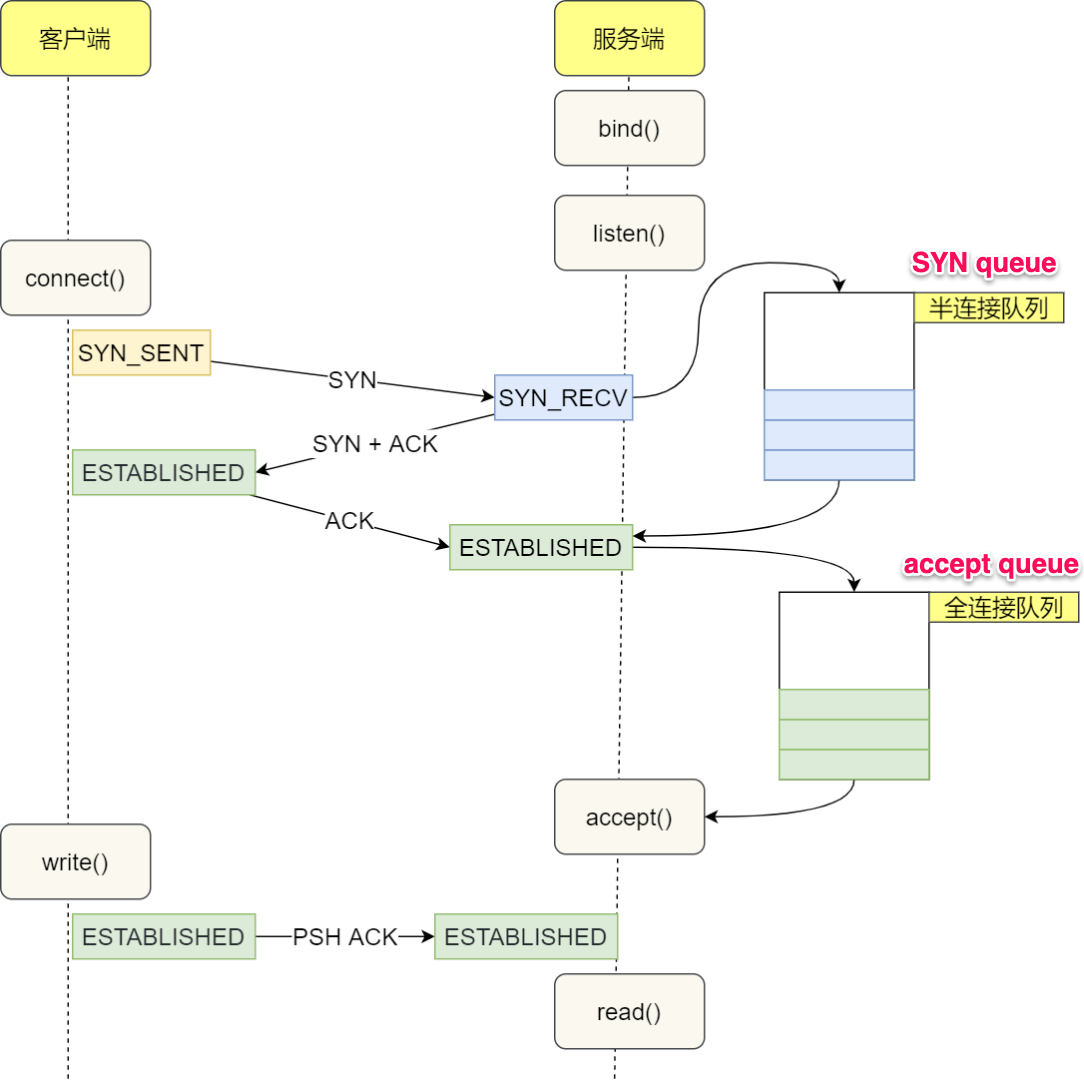
《深入探索 Linux listen() 函数 backlog 的含义》
https://man7.org/linux/man-pages/man2/accept.2.html
SYNOPSIS
2
3
4
5
6
7
// On success, a nonnegative integer that is a file descriptor for the accepted socket is returned.
// On error, -1 is returned, and errno is set appropriately.
int accept(int sockfd,
struct sockaddr *addr,
socklen_t *addrlen)DESCRIPTION
The
accept()system call is used with connection-based socket types (SOCK_STREAM,SOCK_SEQPACKET). It extracts the first connection request on the queue of pending connections for the listening socket, sockfd, creates a new connected socket, and returns a new file descriptor referring to that socket. The newly created socket is not in the listening state. The original socket sockfd is unaffected by this call.If no pending connections are present on the queue, and the socket is not marked as nonblocking,
accept()blocks the caller until a connection is present. If the socket is marked nonblocking and no pending connections are present on the queue,accept()fails with the error EAGAIN or EWOULDBLOCK.
https://man7.org/linux/man-pages/man2/connect.2.html
SYNOPSIS
2
3
4
5
6
7
// If the connection or binding succeeds, 0 is returned.
// On error, -1 is returned, and errno is set appropriately.
int connect(int sockfd,
const struct sockaddr *addr,
socklen_t addrlen);DESCRIPTION
The
connect()function is used by a TCP client to establish a connection with a TCP server.The function returns
0if the it succeeds in establishing a connection (i.e., successful TCP three-way handshake,-1otherwise.The client does not have to call
bind()in Section before calling this function: the kernel will choose both an ephemeral port and the source IP if necessary.
https://man7.org/linux/man-pages/man2/close.2.html
SYNOPSIS
2
3
int close(int fd);
用于完成四次挥手流程:
close() 主动关闭连接,这时 TCP 发送一个 FIN M;EOF 传递给应用进程(此时 recv() 返回值为 0),因为 FIN 的接收意味着应用进程在相应的连接上再也接收不到额外数据)close() 主动关闭它的 socket,这导致它的 TCP 也发送一个 FIN N; 这样每个方向上都有一个 FIN 和 ACK。
SYNOPSIS
DESCRIPTION
getsockopt(2) and setsockopt(2) are used to set or get socket layer or protocol options.
level 常用选项如下:
socket layer
protocol layer
Using the
SOL_IPsocket options level isn’t portable; BSD-based stacks use theIPPROTO_IPlevel.
https://man7.org/linux/man-pages/man7/socket.7.html
SO_RCVTIMEO and SO_SNDTIMEO
Specify the receiving or sending timeouts until reporting an error. The argument is a struct timeval.
Return value:
- If an input or output function blocks for this period of time, and data has been sent or received, the return value of that function will be the amount of data transferred;
- if no data has been transferred and the timeout has been reached, then -1 is returned with errno set to EAGAIN or EWOULDBLOCK, or EINPROGRESS (for connect(2)) just as if the socket was specified to be nonblocking.
Timeout setting:
- If the timeout is set to zero (the default) then the operation will never timeout.
- Timeouts only have effect for system calls that perform socket I/O (e.g., read(2), recvmsg(2), send(2), sendmsg(2));
- timeouts have no effect for select(2), poll(2), epoll_wait(2), and so on.
2
setsockopt(clientfd, SOL_SOCKET, SO_SNDTIMEO, ...);
<How to set socket timeout in C when making multiple connections?>
<Why there is no “write timeout” for the socket ?>
SO_RCVBUF
Sets or gets the maximum socket receive buffer in bytes. The kernel doubles this value (to allow space for bookkeeping overhead) when it is set using setsockopt(2), and this doubled value is returned by getsockopt(2). The default value is set by the /proc/sys/net/core/rmem_default file, and the maximum allowed value is set by the /proc/sys/net/core/rmem_max file. The minimum (doubled) value for this option is 256.
SO_SNDBUF
Sets or gets the maximum socket send buffer in bytes. The kernel doubles this value (to allow space for bookkeeping overhead) when it is set using setsockopt(2), and this doubled value is returned by getsockopt(2). The default value is set by the /proc/sys/net/core/wmem_default file and the maximum allowed value is set by the /proc/sys/net/core/wmem_max file. The minimum (doubled) value for this option is 2048.
SO_REUSEADDR
Indicates that the rules used in validating addresses supplied in a bind(2) call should allow reuse of local addresses. For AF_INET sockets this means that a socket may bind, except when there is an active listening socket bound to the address. When the listening socket is bound to INADDR_ANY with a specific port then it is not possible to bind to this port for any local address. Argument is an integer boolean flag.
SO_REUSEPORT (since Linux 3.9)
《深入理解 Linux 端口重用这一特性——良许 Linux》
https://man7.org/linux/man-pages/man7/tcp.7.html
SO_KEEPALIVE 开启 TCP keepalive
Enable sending of keep-alive messages on connection-oriented sockets. Expects an integer boolean flag.
TCP keepalive 具体参数设置:
TCP_KEEPCNT: overrides tcp_keepalive_probes
TCP_KEEPIDLE: overrides tcp_keepalive_time
TCP_KEEPINTVL: overrides tcp_keepalive_intvl
2
3
setsockopt(clientfd, IPPROTO_TCP, TCP_KEEPIDLE, ...);
setsockopt(clientfd, IPPROTO_TCP, TCP_KEEPINTVL, ...);
TCP_NODELAY
If set, disable the Nagle algorithm. This means that segments are always sent as soon as possible, even if there is only a small amount of data. When not set, data is buffered until there is a sufficient amount to send out, thereby avoiding the frequent sending of small packets, which results in poor utilization of the network.
成功建立连接之后,双方开始通过 recv() 和 send() 来读、写数据,就像往一个文件流里面写东西一样。
https://man7.org/linux/man-pages/man2/recv.2.html
https://man7.org/linux/man-pages/man2/recvfrom.2.html
https://man7.org/linux/man-pages/man2/recvmsg.2.html
receive a message from a socket
- If no messages are available at the socket, the receive calls wait for a message to arrive, unless the socket is nonblocking (see fcntl(2)), in which case the value -1 is returned and the external variable errno is set to EAGAIN or EWOULDBLOCK.
- The select(2) or poll(2) call may be used to determine when more data arrives.
1 | #include <sys/socket.h> |
https://man7.org/linux/man-pages/man2/send.2.html
https://man7.org/linux/man-pages/man2/sendto.2.html
https://man7.org/linux/man-pages/man2/sendmsg.2.html
send a message on a socket
- When the message does not fit into the send buffer of the socket, send() normally blocks, unless the socket has been placed in nonblocking I/O mode. In nonblocking mode it would fail with the error EAGAIN or EWOULDBLOCK in this case.
- The select(2) call may be used to determine when it is possible to send more data.
1 | #include <sys/socket.h> |
默认设置下,socket 为同步阻塞 I/O 模型,下列系统调用会引发阻塞:
| Call type | Socket state | blocking | Nonblocking |
|---|---|---|---|
Types of recv() calls |
Input is available | Immediate return | Immediate return |
| No input is available | Wait for input | Immediate return with EWOULDBLOCK error number |
|
Types of send() calls |
Output buffers available | Immediate return | Immediate return |
| No output buffers available | Wait for output buffers | Immediate return with EWOULDBLOCK error number |
|
accept() call |
New connection | Immediate return | Immediate return |
| No connections queued | Wait for new connection | Immediate return with EWOULDBLOCK error number |
|
connect() call |
Wait | Immediate return with EINPROGRESS error number |
有几种设置方式可以将 socket 设置为同步非阻塞 I/O 模型:
使用 fcntl(2) + O_NONBLOCK 参数。POSIX 标准,版本兼容性最好,推荐使用:
1 | int flags = fcntl(listenfd, F_GETFL, 0); |
使用 ioctl(2) + FIONBIO 参数。版本兼容性较弱,不建议使用:
1 | int on = 1; |
从 Linux 2.6.27 开始,也可以使用 socket(2) 和 accept4(2) 直接创建非阻塞 socket:
1 | int listenfd, clientfd; |
上述几个文件描述符 fd 的基础概念:
bind() 地址和端口,调用 listen() 函数发起侦听的一端;accept() 函数接受新连接,由 accept() 函数返回的 socket。accept() 函数并不参与三次握手过程,accept() 函数从已经完成连接的 backlog 队列中取出连接,并返回 clientfd;connect() 函数主动发起连接(三次握手)的一端。最后客户端与服务端分别通过 connfd 和 clientfd 进行通信(调用 send() 或者 recv() 函数)。
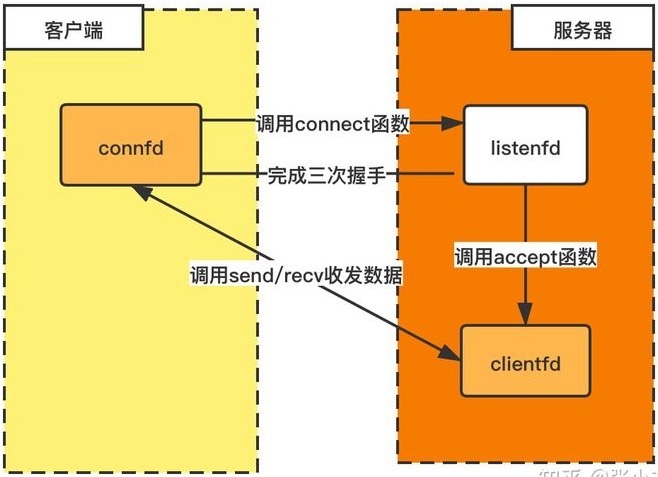
https://cs.dartmouth.edu/~campbell/cs60/socketprogramming.html
https://www.geeksforgeeks.org/socket-programming-cc/
https://github.com/qidawu/cpp-data-structure/tree/main/socket
https://en.wikipedia.org/wiki/Network_socket
https://en.wikipedia.org/wiki/Berkeley_sockets
<Client/server socket programs: Blocking, nonblocking, and asynchronous socket calls | IBM>
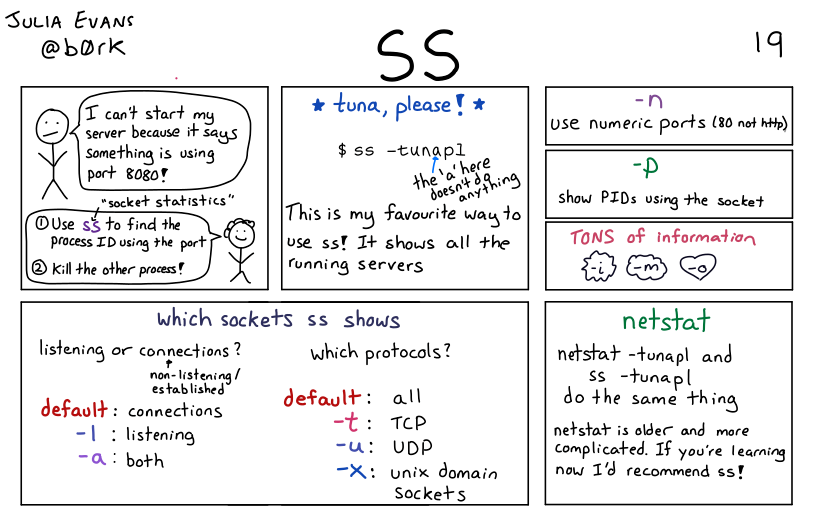
https://man7.org/linux/man-pages/man8/ss.8.html
1 | ss [options] [ FILTER ] |

1 | # 列出当前 socket 统计信息 |
1 | # 统计指定进程 TCP 连接占用的端口 |
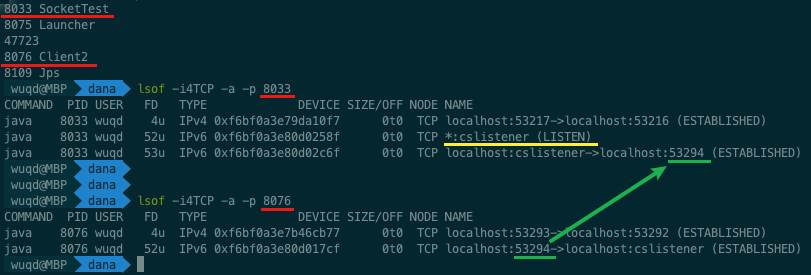
ss、netstat、lsof 命令的输出结果对比netstat 是遍历 /proc 下面每个 PID 目录;
ss 直接读 /proc/net 下面的统计信息。所以 ss 执行的时候消耗资源以及消耗的时间都比 netstat 少很多。
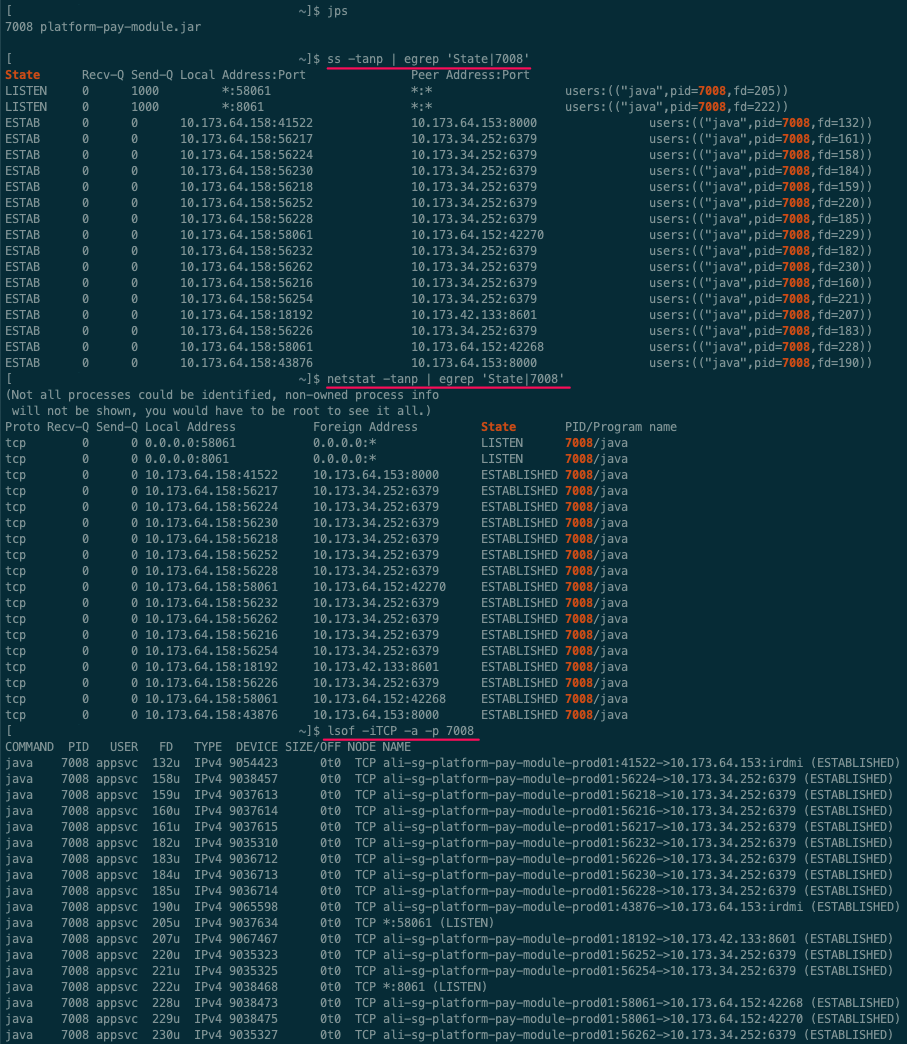
https://en.wikipedia.org/wiki/Netstat
https://linux.die.net/man/8/netstat
1 | $ netstat -tanp | grep 7059 | tr -s ' ' | cut -d ' ' -f 4 | sort -n | uniq -c |
1 | $ netstat -anv | grep 7059 |
1 | # 查询占用了 8080 端口的[进程号](最后一列) |
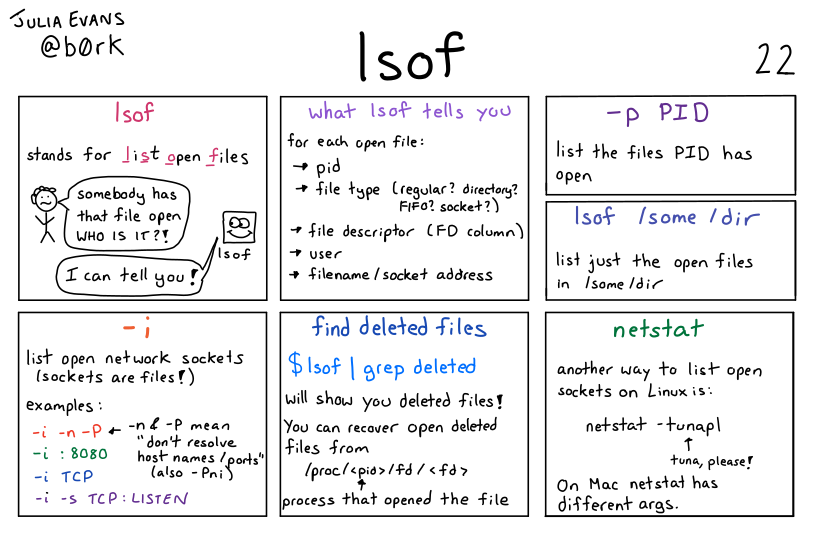
https://en.wikipedia.org/wiki/Lsof
https://linux.die.net/man/8/lsof
常用选项:
| 选项 | 描述 |
|---|---|
| -n | 不显示主机名(host name),显示 IP(network number)。例如 localhost 显示为 127.0.0.1 |
| -P | 不显示端口名(port name),显示端口号(port number)。例如 cslistener 显示为 9000 |
| -a | AND 运算 |
| -p s | 筛选指定 PID |
| -i […] | 筛选指定条件,例如:TCP + 端口号 |
| -s [p:s] | 筛选指定条件:例如:TCP (LISTEN) |
-i [
46][protocol][@hostname|hostaddr][:service|port]where:
46specifies the IP version, IPv4 or IPv6 that applies to the following address. ‘6‘ may be be specified only if the UNIX dialect supports IPv6. If neither ‘4‘ nor ‘6‘ is specified, the following address applies to all IP versions.protocolis a protocol name -TCP,UDPhostnameis an Internet host name. Unless a specific IP version is specified, open network files associated with host names of all versions will be selected.hostaddris a numeric Internet IPv4 address in dot form; or an IPv6 numeric address in colon form, enclosed in brackets, if the UNIX dialect supports IPv6. When an IP version is selected, only its numeric addresses may be specified.serviceis an /etc/services name - e.g.,smtpor a list of them.portis a port number, or a list of them.Here are some sample addresses:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
-iTCP:25 - TCP and port 25
-i@1.2.3.4 - Internet IPv4 host address 1.2.3.4
-i@[3ffe:1ebc::1]:1234 - Internet IPv6 host address 3ffe:1ebc::1, port 1234
-iUDP:who - UDP who service port
-iTCP@lsof.itap:513 - TCP, port 513 and host name lsof.itap
-iTCP@foo:1-10,smtp,99 - TCP, ports 1 through 10, service name smtp, port 99, host name foo
-iTCP@bar:1-smtp - TCP, ports 1 through smtp, host bar
-i:time - either TCP, UDP or UDPLITE time service port
-s [p:s]
When followed by a protocol name (p), either
TCPorUDP, a colon (‘:’) and a comma-separated protocol state name list, the option causes open TCP and UDP files to be
- excluded if their state name(s) are in the list (s) preceded by a ‘^’;
or
- included if their state name(s) are not preceded by a ‘^’.
For example, to list only network files with
TCPstateLISTEN, use:
State names vary with UNIX dialects, so it’s not possible to provide a complete list. Some common TCP state names are:
CLOSED,IDLE,BOUND,LISTEN,ESTABLISHED,SYN_SENT,SYN_RCDV,ESTABLISHED,CLOSE_WAIT,FIN_WAIT1,CLOSING,LAST_ACK,FIN_WAIT_2, andTIME_WAIT.
1 | # 筛选条件:端口号 |
1 | # 查看某个进程的 open files,等价于 /proc/PID/fd/ |
lsof 输出结果每一列的含义:
COMMAND:进程的名称
PID:进程标识符
USER:进程所有者
FD:文件描述符,应用程序通过文件描述符识别该文件。如 cwd、txt 等
TYPE:文件类型,如 DIR、REG 等
DEVICE:指定磁盘的名称
SIZE:文件的大小
NODE:索引节点(文件在磁盘上的标识〉
NAME:打开文件的确切名称