数据结构系列（三）树结构总结

相关术语

维基百科 Tree (data structure) 的相关术语：

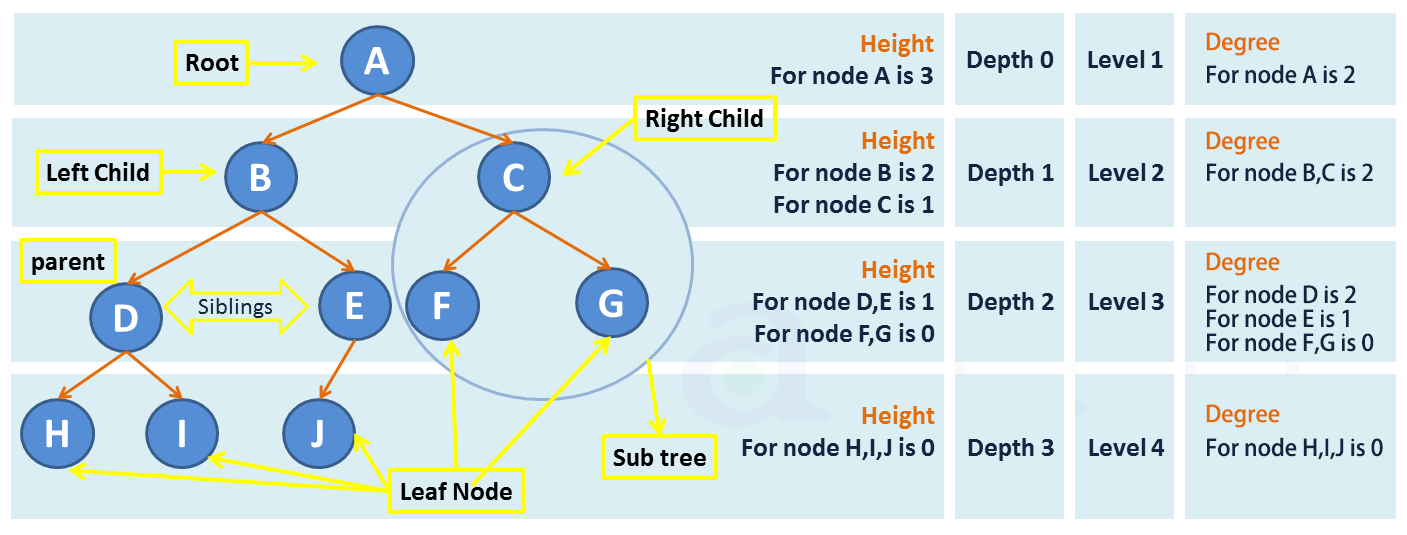
• 结点（Node）：包含一个数据元素及若干指向其子树的分支。

• 结点的度（Degree of node）：

  For a given node, its number of children. A leaf has necessarily degree zero.

• 树的度（Degree of tree）：

  The degree of a tree is the maximum degree of a node in the tree.

• 高度（Height）、深度（Depth）：

  The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree.

  The depth of a node is the length of the path to its root (i.e., its root path).

  

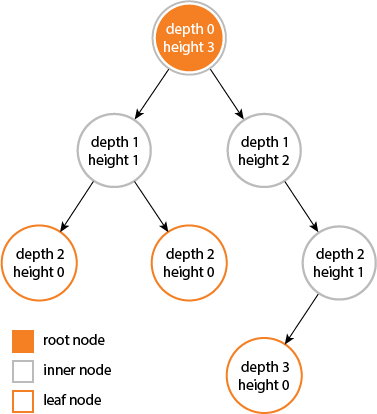
  When using zero-based counting, the root node has depth zero, leaf nodes have height zero, and a tree with only a single node (hence both a root and leaf) has depth and height zero. Conventionally, an empty tree (tree with no nodes, if such are allowed) has height −1.

参考：

https://www.baeldung.com/cs/tree-depth-height-difference

https://stackoverflow.com/questions/2603692/what-is-the-difference-between-tree-depth-and-height

一叉树

有没有想过为啥有二叉树，而没有一叉树？实际上顺序表、链式表就是特殊的树，即一叉树实现。

二叉树

二叉树的五种基本形态：

注意：一棵树（包括二叉树）的最少结点个数为 0（空树）。

二叉树的常见形态：

1. 二叉树
2. 满二叉树
3. 完全二叉树

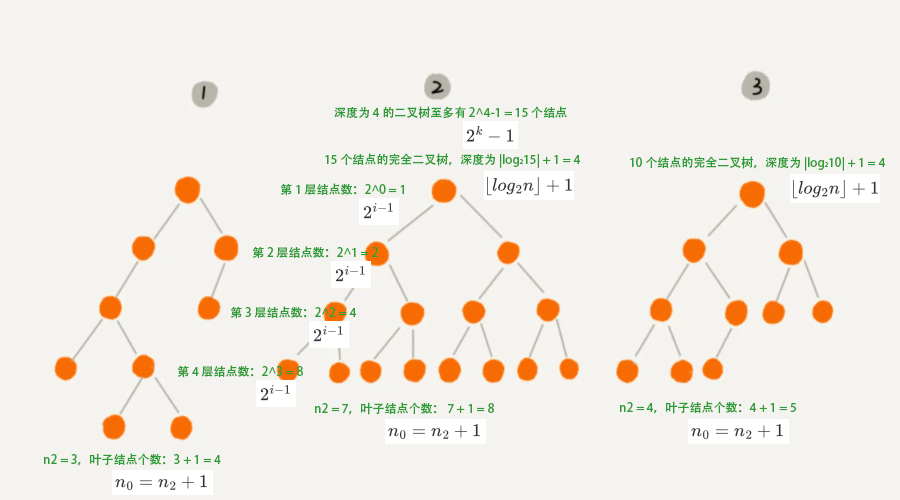
二叉树的通用性质：

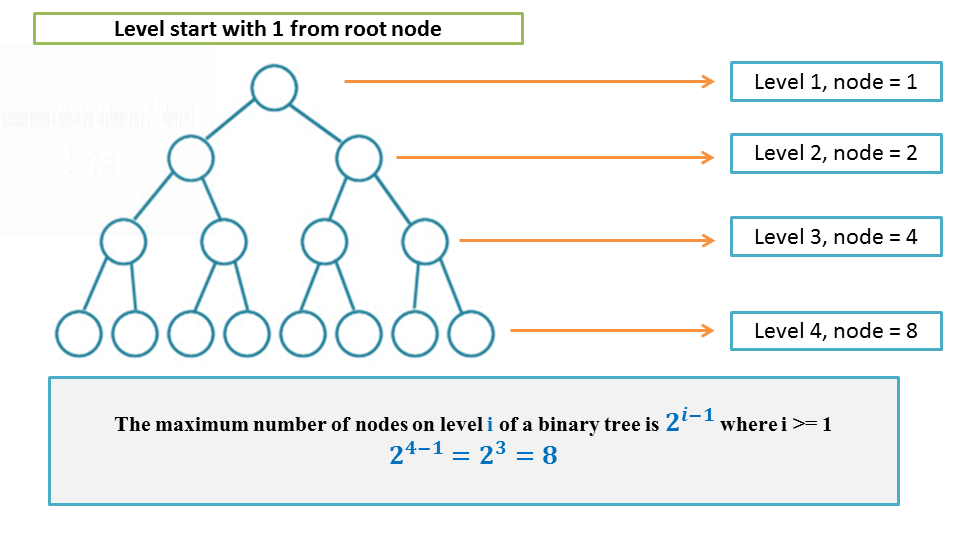
• 性质 1：二叉树第 i (i ≥ 1) 层至多有 $2^{i-1}$ 个结点。

  

• 性质 2：深度为 k (k ≥ 1) 的二叉树至多有 $2^k-1$ 个结点。

  

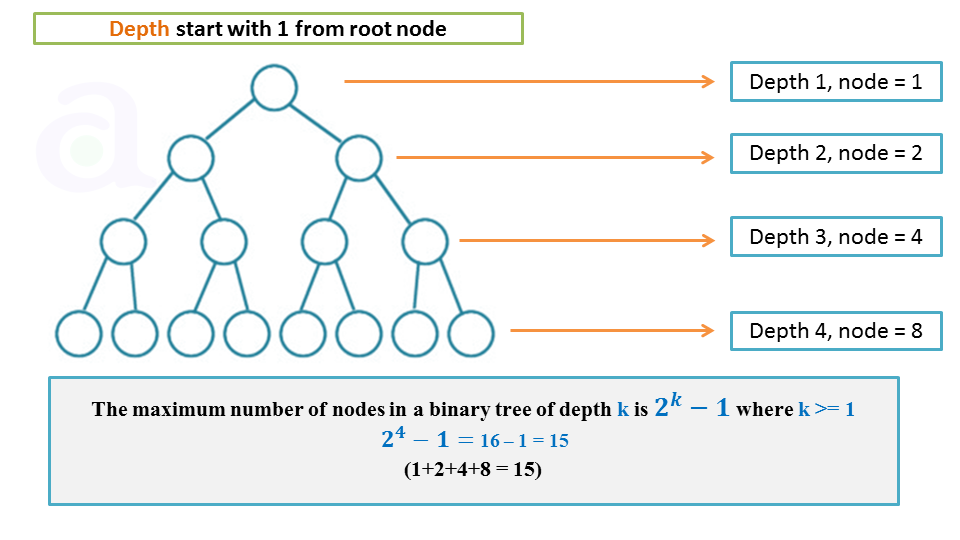
• 性质 3：二叉树中，若度数为 0 的叶子结点个数为 $n_0$，度数为 2 的结点个数为 $n_2$，则 $n_0 = n_2 + 1$。

• 若根节点的层数为 1，则具有 n 个结点的二叉树的最大高度为 n（即一叉树）。

参考：https://www.atnyla.com/tutorial/level-and-height-of-the-tree/3/392

逻辑结构

下面介绍几种特殊的二叉树：

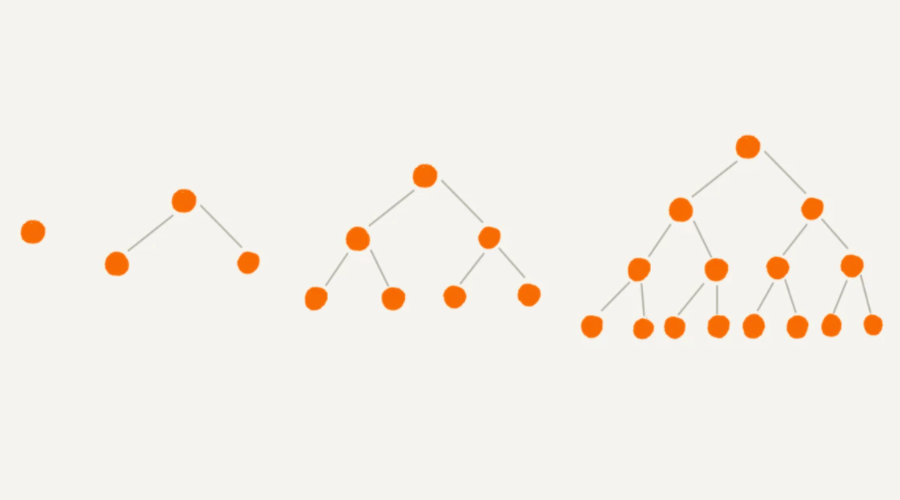
满二叉树（Full Binary Tree）

满二叉树的性质：

• 深度为 k (k ≥ 1) 的满二叉树，共有 $2^k-1$ 个结点。如下图和表格：

  

  	$k=1$	$k=2$	$k=3$	$k=4$
  结点总数	$2^1-1=1$	$2^2-1=3$	$2^3-1=7$	$2^4-1=15$

完全二叉树（Complete Binary Tree）

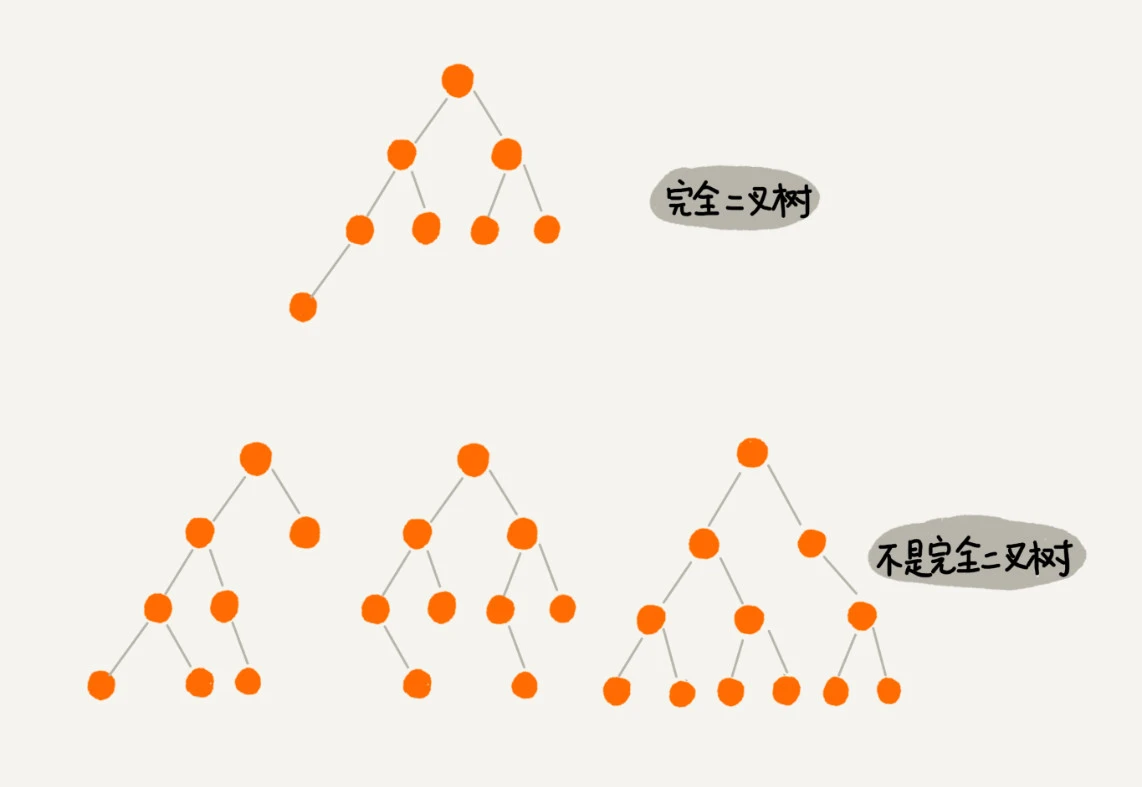
完全二叉树的性质：

• 含有 n 个结点的完全二叉树，深度为 $⌊log_2n⌋+1$。

• 深度为 k 的完全二叉树：

  	$k=1$	$k ≥ 2$
  最少结点数	$2^{k-1}$	$2^{k-1}$
  最少叶子结点数	$k$	$2^{k-2}$

  如下图和表格：

  

  	$k=1$	$k=2$	$k=3$	$k=4$
  最少结点数	$2^{1-1}=1$	$2^{2-1}=2$	$2^{3-1}=4$	$2^{4-1}=8$
  最少叶子结点树	1	$2^{2-2}=1$	$2^{3-2}=2$	$2^{4-2}=4$

• 含有 n 个结点的完全二叉树按层编号，则：

存储结构

顺序存储结构

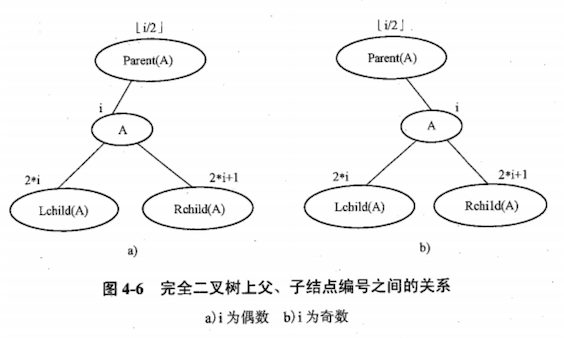
如果将完全二叉树按层编号，并以编号作为数组下标将结点存入一维数组中，则完全二叉树的顺序存储结构如下图：

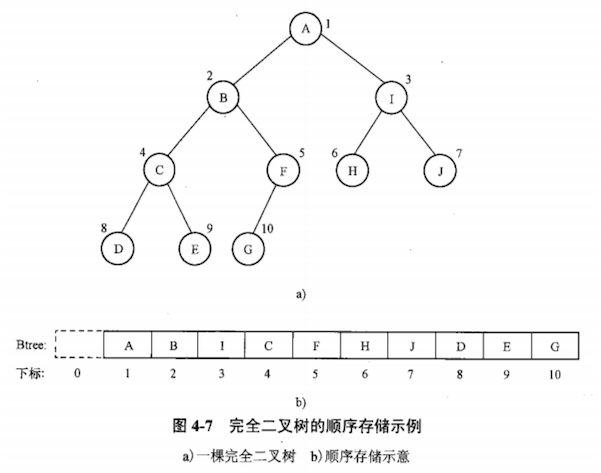
通过观察，完全二叉树按层编号之后，编号之间的关系满足下图的编号计算公式。

公式可以准确反映出结点之间的逻辑关系，可用于求某结点的父、子结点。（这一性质是二叉树顺序存储结构的基础）

但如果将非完全二叉树按层编号进行顺序存储，则无法套用编号计算公式求父、子结点：

	优点	缺点
方式一：直接对结点按层编号，然后再将各结点按编号存入数组。	节省存储空间。	无法根据结点间的下标关系确定它们之间的逻辑关系，从而难以实现二叉树求父、子结点等基本运算。
方式二：先增设虚拟节点，将其转为一棵完全二叉树，然后再按层编号存入数组。	方便实现二叉树求父、子结点等基本运算。	浪费存储空间。

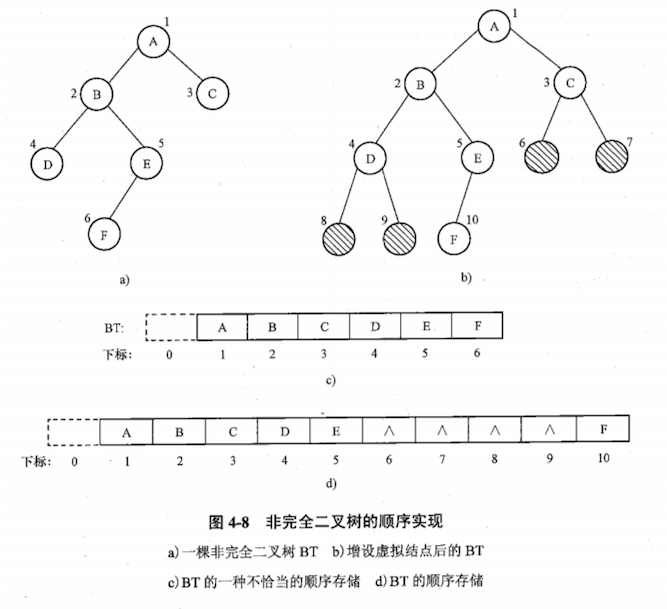
所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。

当我们讲到堆和堆排序的时候，你会发现，堆其实就是一种完全二叉树，最常用的存储方式就是数组。

链式存储结构

二叉树有不同的链式存储结构，其中最常用的是二叉链表和三叉链表，其结点形式如下图：

二叉树的两种链式存储结构如下图：

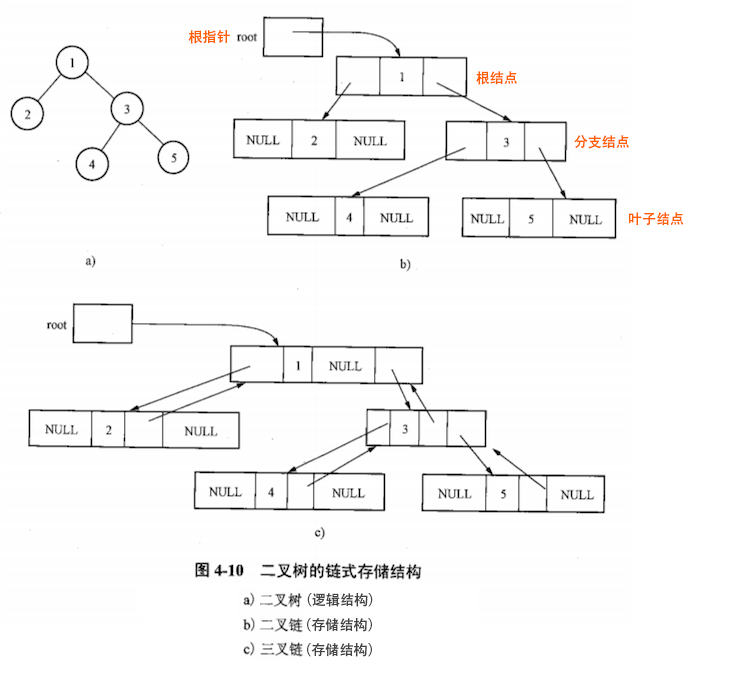
其中，判断叶子结点的条件为：(p->lchild == NULL) && (p->rchild == NULL)。

基本运算

树常见的基本运算如下：

• 初始化（Init）
• 建树（Create）
• 插入、删除结点
• 求根（Root）
• 求双亲（Parent）
• 求孩子（Child）
  • 二叉树求左孩子（Lchild）
  • 二叉树求右孩子（Rchild）
• 遍历（Traverse）
  • 二叉树先序遍历（PreOrderTraverse）
  • 二叉树中序遍历（InOrderTraverse）
  • 二叉树后序遍历（PostOrderTraverse）
  • 层次遍历（LevelOrder）：从上往下逐层遍历，同一层中结点从左往右

遍历

https://en.wikipedia.org/wiki/Tree_traversal

• https://en.wikipedia.org/wiki/Depth-first_search
• https://en.wikipedia.org/wiki/Breadth-first_search

已知二叉树，求遍历序列

二叉树的遍历（traversing binary tree），是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问有且仅被访问一次。

二叉树的遍历，有三种经典方式：

经典的三种遍历方式	遍历顺序	推导
先序遍历	DLR	首先访问父节点，因此先序序列的第一个结点必为根节点 （如下图先序遍历 A）
中序遍历	LDR	先于根结点的为左子树，后于根结点的为右子树
后序遍历	LRD	最后访问父节点，因此后序序列的最后一个结点必为根节点 （如下图后序遍历 A）

已知二叉树，求三种遍历序列：

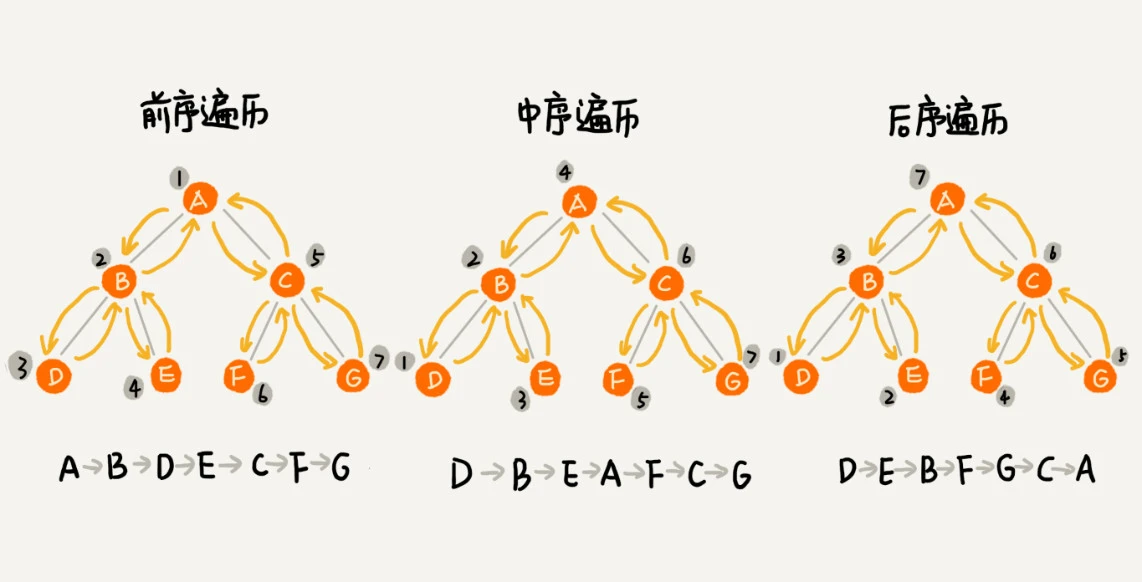
归纳：

• 若一棵非空二叉树的先序序列和后序序列相同，则该二叉树中只有一个根节点。
• 若一棵具有 n (n>0) 个结点的二叉树的先序序列和后序序列正好相反，则该二叉树一定是：高度为 n 的二叉树。
• 若一棵二叉树的先序序列和中序序列正好相反，则二叉树上每个结点的右子树都是空二叉树。

已知遍历序列，求二叉树

由二叉树的遍历可知，任意一棵二叉树结点的先序序列、中序序列和后序序列都是唯一的。已知先序或后序序列 + 中序序列，可以确定一棵二叉树：

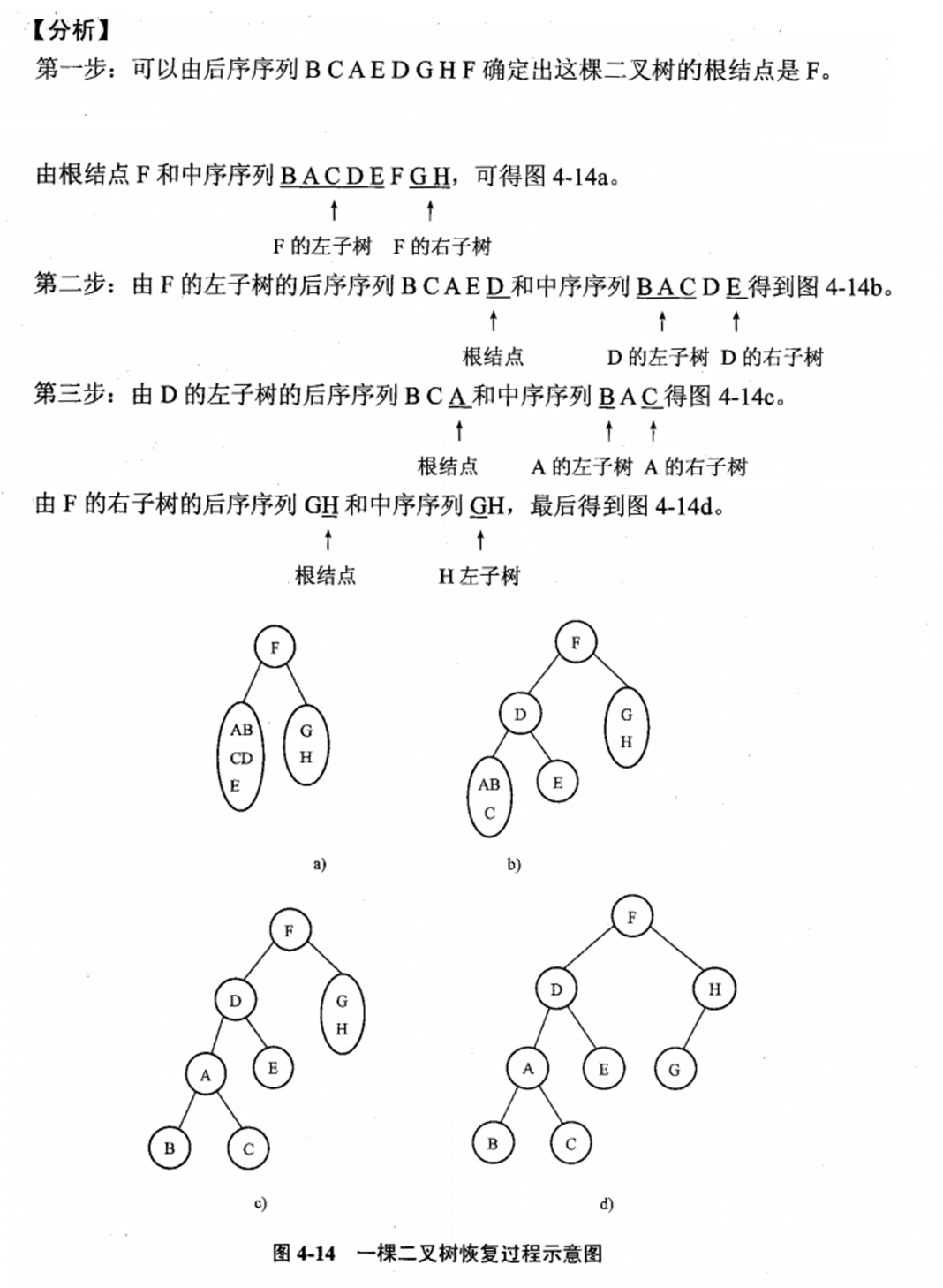
问题：

• 假设一棵二叉树的中序序列与后序序列分别为：BACDEFGH 和 BCAEDGHF，建立该二叉树。

分析：

二叉树遍历的实现方式

• 递归实现
• 非递归实现（栈）

多叉树

B-tree

B-tree 的阶（Order），来自 Knuth (1998) 的定义：

Knuth (1998) defining the order to be maximum number of children (which is one more than the maximum number of keys).

所以按照 Knuth 定义一棵 m 阶的 B 树（国内教材所用的定义）：

Every node has at most m children.

每个节点最多有 m 个孩子。

Every non-leaf node (except root) has at least ⌈m/2⌉ child nodes.

非叶非根节点至少有 [m/2] 个儿子。[m/2] 表示取大于 m/2 的最小整数。

The root has at least two children if it is not a leaf node.

根节点至少有 2 个儿子。除非它本身是叶子节点，即整棵树只有它一个节点。

A non-leaf node with k children contains k − 1 keys.

非叶节点：有 k 个儿子，就有 k-1 个 keys。

All leaves appear in the same level and carry no information.

所有叶子节点在同一层，不携带信息 data。

例如一棵 3 阶 B 树，高度相比二叉树会更低。

B+ Tree

特性：

• 非叶子节点存储索引；
• 叶子节点存储数据，且通过双向链表关联。

为什么用？

• 为了减少内存开销和磁盘 IO

  B+树非叶子节点上是不存储数据的，仅存储键值，而B树节点中不仅存储键值，也会存储数据。之所以这么做是因为在数据库中页的大小是固定的，innodb中页的默认大小是16KB。如果不存储数据，那么就可以存储更多的键值，相应的树的阶数就会更大，树就会更矮更胖，如此一来我们查找数据进行磁盘的IO次数会再次减少，数据查询的效率也会更快。另外，B+树的阶数是等于键值的数量的，如果我们的B+树一个节点可以存储1000个键值，那么3层B+树可以存储1000×1000×1000=10亿个数据。一般根节点是常驻内存的，所以一般我们查找10亿数据，只需要2次磁盘IO。

• 为了支持区间查找

  因为B+树索引的所有数据均存储在叶子节点，而且数据是按照顺序排列的，叶子节点间通过双向链表连接。那么B+树使得范围查找，排序查找，分组查找以及去重查找变得异常简单。而B树因为数据分散在各个节点，要实现这一点是很不容易的。

树和森林

https://en.wikipedia.org/wiki/Tree_structure

逻辑结构

无回路的连通图（Connected Graph）即为树。

存储结构

森林（Forest）：n 棵互不相交的树的集合。

A set of n ≥ 0 disjoint trees.

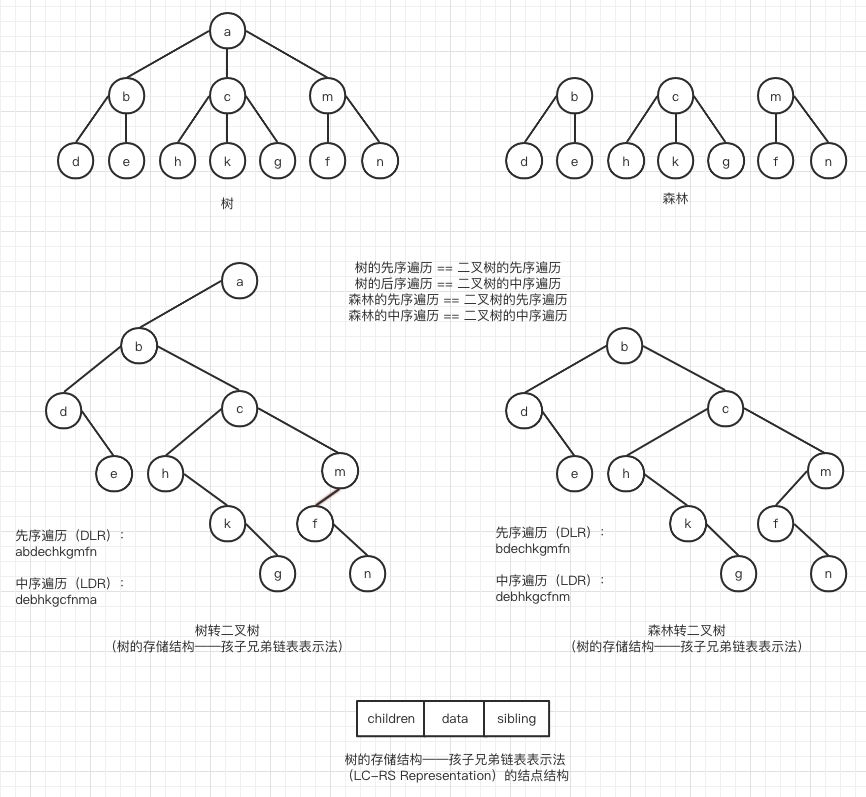
https://blog.csdn.net/chengyq116/article/details/112342319

https://slidetodoc.com/left-childright-sibling-representation-instructor-prof-jyhshing-roger/

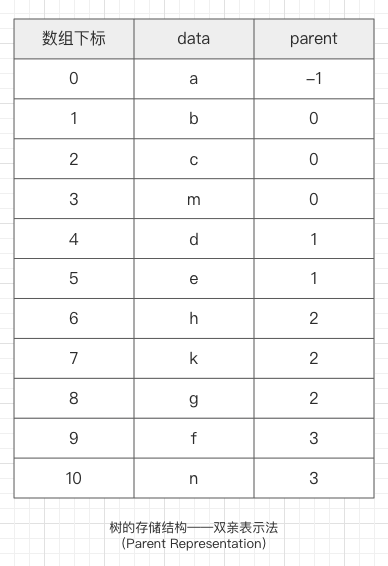
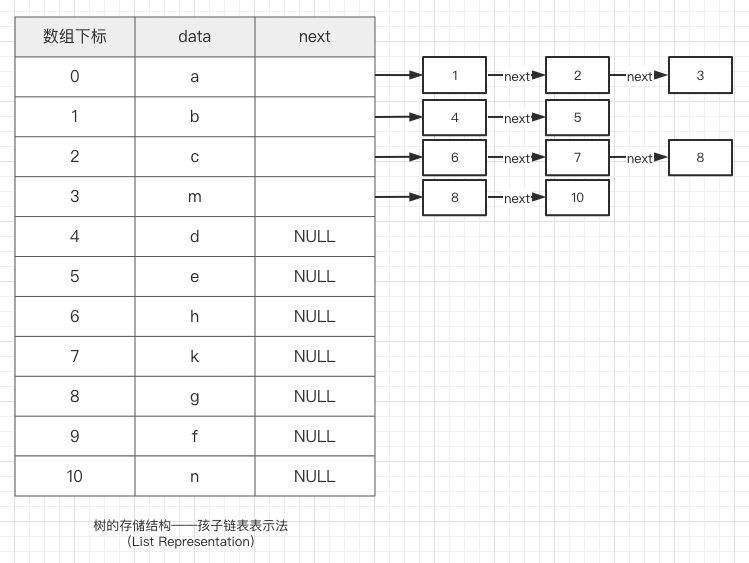
树的应用

分类算法

哈夫曼树（最优二叉树）

https://en.wikipedia.org/wiki/Huffman_tree

哈夫曼树的性质：

• 哈夫曼树中，不存在度数为 1 的分支结点。
• 若度数为 0 的叶子结点个数为 $n_0$，则哈夫曼树共有 $2n_0 - 1$ 个结点。
• 若度数为 2 的结点个数为 $n_2$，则哈夫曼树共有 $2(n_2 + 1) - 1$ 个结点。

《灵光一现的创造 霍夫曼编码》

【霍夫曼编码原理 文本压缩、ZIP压缩文件原理 Huffman Encoding by Tom Scott-哔哩哔哩】 https://b23.tv/wFatkFc

【Huffman 编码动画演示】 https://www.bilibili.com/video/BV18V411v7px/

查找

二叉查找树（Binary Search Tree, BST）

中序遍历时从小到大的二叉树。

平衡二叉查找树（Balanced Binary Search Tree, BBST）

排序

堆排序（Heap）

《28 | 堆和堆排序：为什么说堆排序没有快速排序快？》

《29 | 堆的应用：如何快速获取到 Top 10 最热门的搜索关键词？》

参考

Tree (data structure)

• Binary tree

  • Binary search tree
    • Self-balancing binary search tree
      • 2–3 tree
      • AA tree
      • AVL tree
      • B-tree
      • Red–black tree
      • Scapegoat tree
      • Splay tree
      • Tango tree
      • Treap
      • Weight-balanced tree

• B-tree

  B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children.[2]Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as disks. It is commonly used in databases and file systems.

  • B+ tree can be viewed as a B-tree in which each node contains only keys (not key–value pairs), and to which an additional level is added at the bottom with linked leaves.

    The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context — in particular, filesystems. This is primarily because unlike binary search trees, B+ trees have very high fanout (number of pointers to child nodes in a node,[1] typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree.

  • 2–3 tree is a B–tree of order 3.

  • 2–3–4 tree is a B–tree of order 4.

• R-tree，R 树是 B 树向多维空间发展的另一种形式

  • Priority R-tree
  • R* tree
  • R+ tree
  • RR* tree
  • Hilbert R-tree
  • X-tree

《23 | 二叉树基础（上）：什么样的二叉树适合用数组来存储？》

《24 | 二叉树基础（下）：有了如此高效的散列表，为什么还需要二叉树？》

《48 | B+树：MySQL数据库索引是如何实现的？》

《AVL树，红黑树，B树，B+树，Trie树都分别应用在哪些现实场景中？》

《Implementing a Binary Tree in Java | Baeldung》