数据结构系列（二）线性结构总结

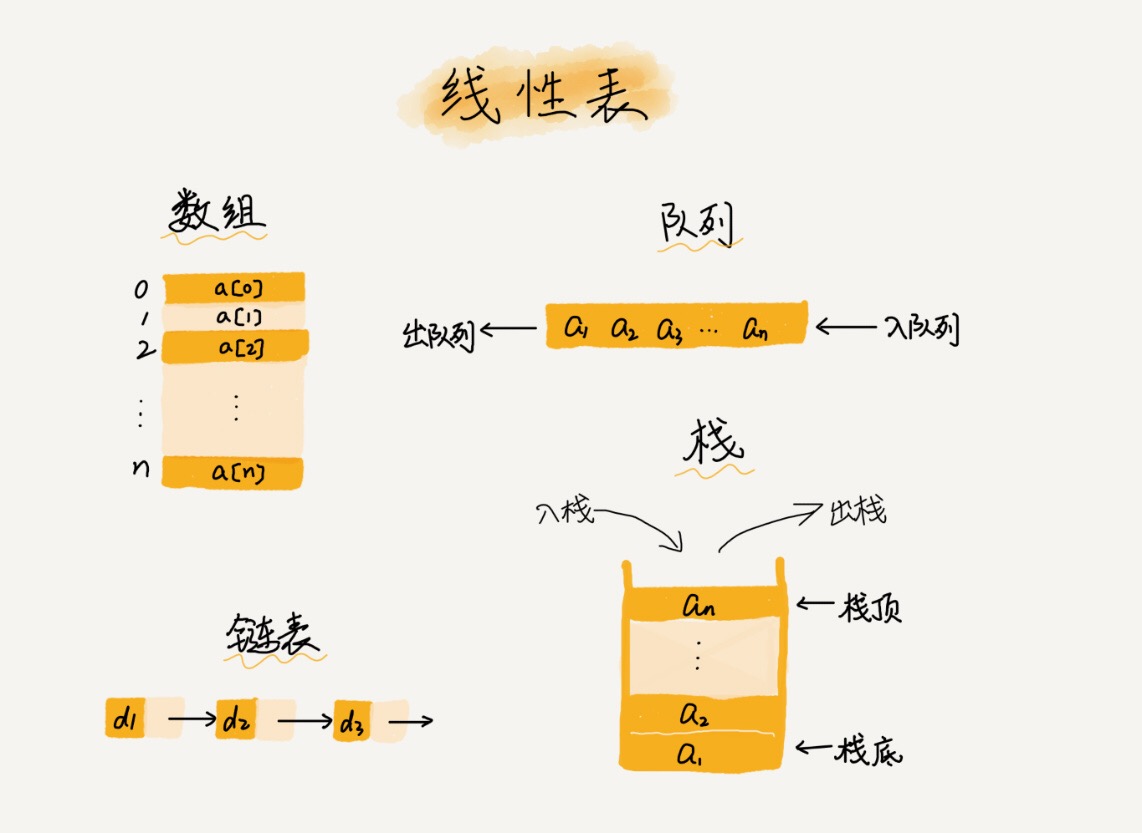
数组

线性表顺序存储的方法是：将表中的结点依次存放在计算机内存中一组连续的存储单元中，数据元素在线性表中的邻按关系决定它们在存储空间中的存储位置，即：逻辑结构中相邻的结点其存储位置也相邻。用顺序存储实现的线性表称为顺序表。一般使用数组来表示顺序表。因此，数组可以看成线性表的一种推广。

一维数组

存储结构

一维数组又称向量（Vector），它由一组具有相同类型的数据元素组成，并存储在一组连续的存储单元中。其存储结构如下图：

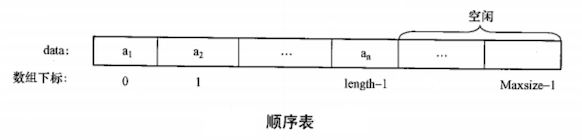
基本运算

对于可变长数组（Resizable Array）的插入、删除操作，其元素移动情况如下：

	元素移动次数 （n 为数组大小, i 为操作位置）	平均移动次数	时间复杂度
插入	$n-i+1$ 次	$n/2$ 次	O(n)
删除	$n-i$ 次	$(n-1)/2$ 次	O(n)

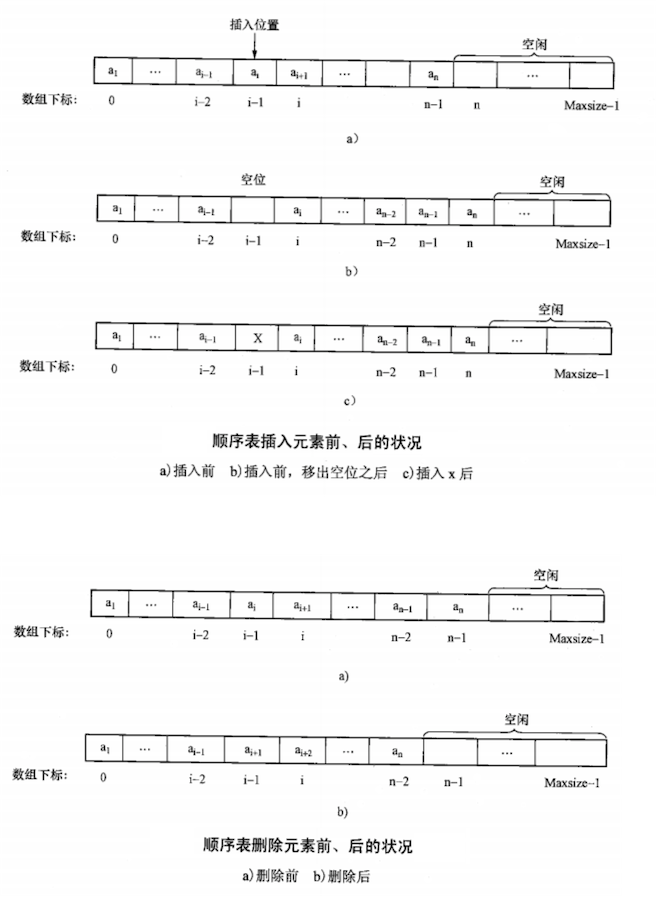
二维数组

若一维数组中的数据元素又是一维数组结构，则称为二维数组，以此类推。一般地，一个 n 维数组可以看成元素为 n-1 维数组的线性表。

二维数组的地址计算（行优先）如下：

$$
loc[i,\ j]=loc[0,\ 0]+(n*i+j)*k
$$

其中，$i$ 为行坐标，$j$ 为列坐标，$n$ 为总列数，$k$ 为存储单元。

由公式可知，数组元素的存储位置是下标的线性函数。

矩阵（Matrix）是很多科学计算问题研究的对象，矩阵可以用二维数组来表示。

在数值分析中经常出现一些高阶矩阵，这些高阶矩阵中有许多值相同的元素或者零元素，如果值相同的元素或者零元素在矩阵中的分布有一定规律，称此类矩阵为特殊矩阵。矩阵的非零元素个数很少的矩阵称为稀疏矩阵。

为了节省存储空间，对这类矩阵采用多个值相同的元素只分配一个存储空间，零元素不存储的策略，这一方法称为矩阵的压缩存储。

链表

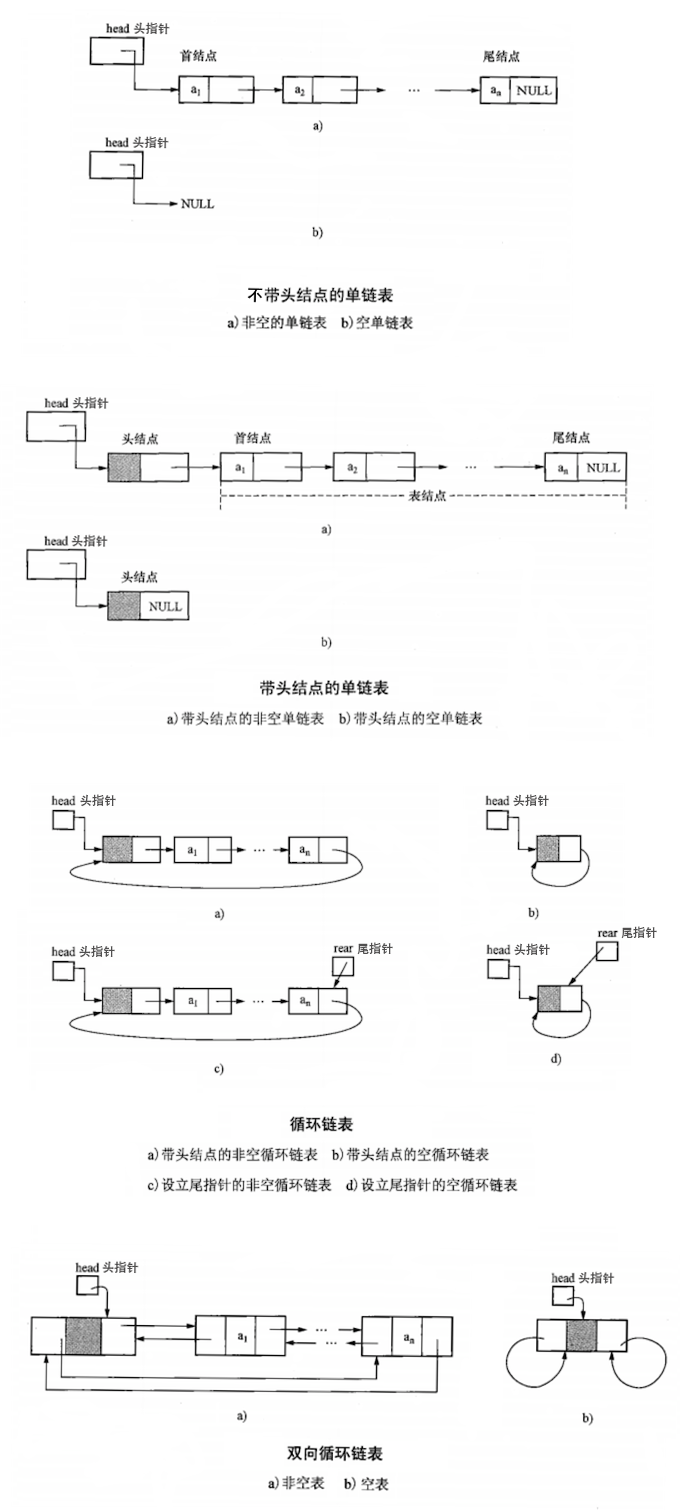
存储结构

四种链表对比：

四种链表	非循环	循环（Cycle）
单向（Singly）	单向链表	单向循环链表
双向（Doubly）	双向链表	双向循环链表

其中，是否循环的关键代码差异如下：

关键代码	非循环链表	循环链表
判断是否空链表	head->next == NULL	head->next == head
判断是否尾结点	p->next == NULL	p->next == head

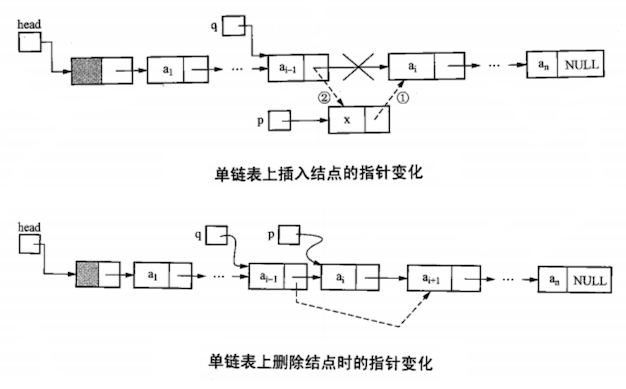
基本运算

单链表插入（insert p before i）、删除（delete i）结点操作如下：

// 单链表需要先找到 i - 1 结点以便进行插入、删除操作
q = get(i - 1);

// 插入结点（注意操作顺序：先新再旧）
p->next = q->next;
q->next = p;

// 删除结点
p = q->next;
q->next = p->next;
free(p);

注意：等号左边是指针，等号右边是结点。

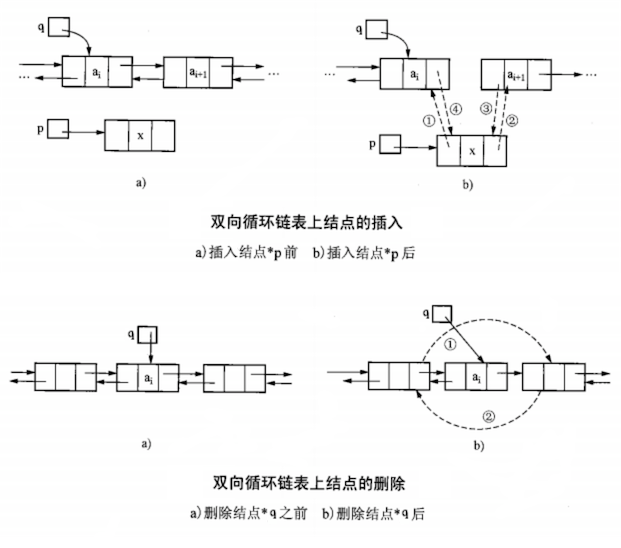
双向循环链表插入（insert p after i）、删除（delete i）结点操作如下：

// 双向循环链表直接获取 i 结点即可，因为可以通过其前驱、后继指针直接进行插入、删除操作
q = get(i);

// 插入结点（注意操作顺序）
p->prev = q;
p->next = q->next;
q->next->prev = p;
q->next = p;

// 删除结点（注意操作顺序）
q->prev->next = q->next;
q->next->prev = q->prev;
free(q);

注意：等号左边是指针，等号右边是结点

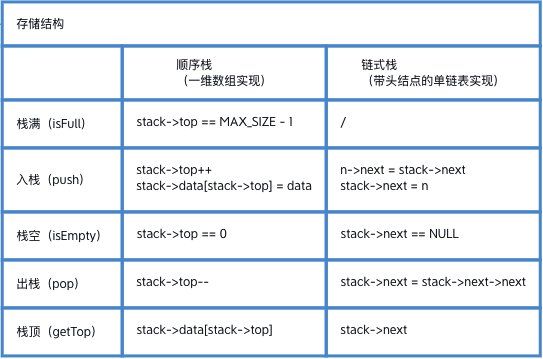
栈

顺序存储结构

链式存储结构

基本运算

使用场景

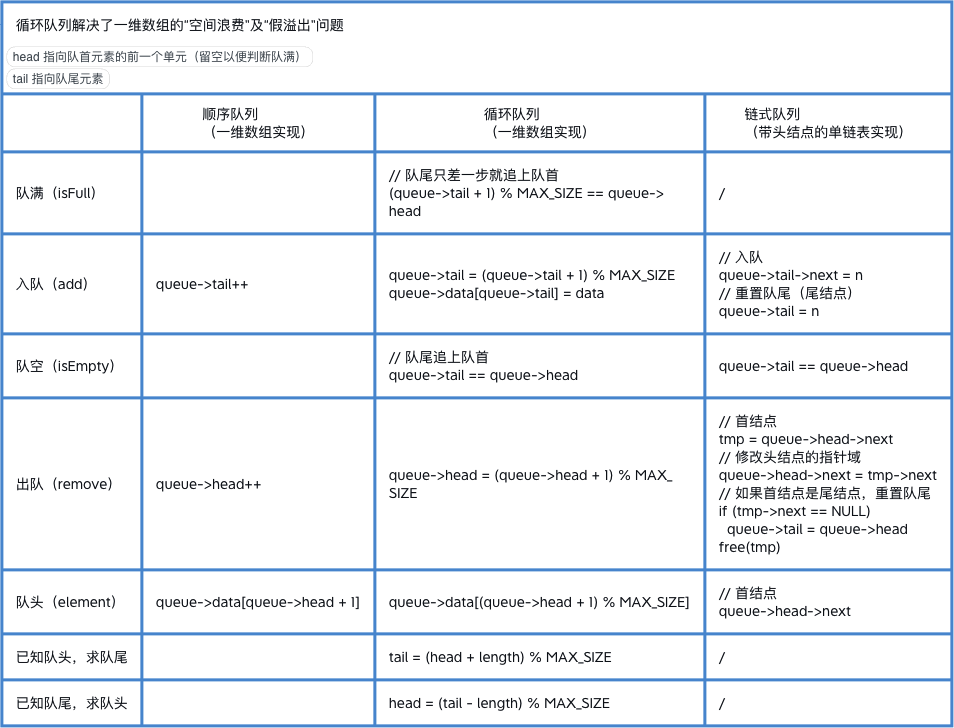
队列

顺序存储结构

链式存储结构

基本运算

使用场景