数据结构系列（四）图、网结构总结

逻辑结构

图的种类

维基百科对图（Graph）的定义：

A graph is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically.

无向图（Undirected Graph）

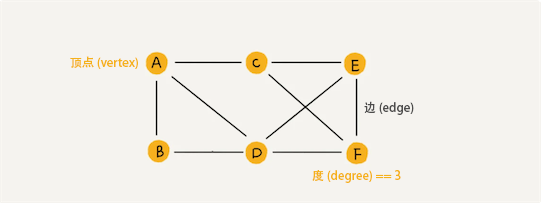
任何两个顶点（vertex）之间都有边（edge）的无向图称为无向完全图。一个具有 n 个顶点的无向完全图的边数为：

$$
C^2_n=n(n-1)/2
$$

有向图（Directed Graph）

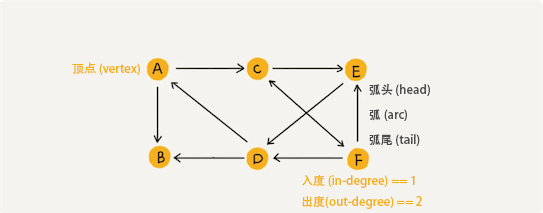
任何两个顶点（vertex）之间都有弧（arc）的有向图称为有向完全图。一个具有 n 个顶点的有向完全图的弧数为：

$$
P^2_n=n(n-1)
$$

带权图（Weighted Graph）

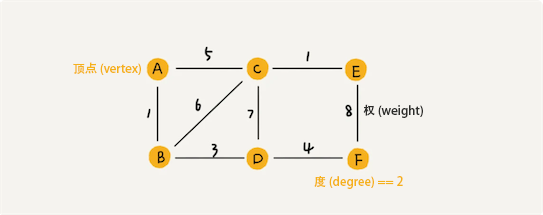
边或弧上带有权值的图，也称为网（network）。

维基百科对网（network）的定义：

In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes (e.g. names).

图（graph）是高度抽象后的逻辑结构，而网（network）在此之上可以通过在顶点（vertex）和边（edge）上增加属性来包含更多的信息，更偏重于对实际问题的建模。

图的相关术语

https://en.wikipedia.org/wiki/Glossary_of_graph_theory

What’s the difference between Adjacency and Connectivity ?

在无向图中，邻接是点与点或者边与边之间的关系。在无向图中，如果两个点之间至少有一条边相连，则称这两个点是邻接的。同样，如果两条边有共同的顶点，则两条边也是邻接的。关联是点与边之自的关系。一个点如果是一条边的顶点之一，则称为点与该边关联。

• https://en.wikipedia.org/wiki/Connectivity_(graph_theory)
• https://en.wikipedia.org/wiki/Glossary_of_graph_theory#adjacent

存储结构

邻接矩阵（Adjacency Matrix）

维基百科对矩阵（Matrix）的定义：

In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.

维基百科对矩阵（Matrix）的定义 2：

数学上，一个 $m×n$ 的矩阵是一个由 $m$ 行（row）$n$ 列（column）元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。

矩阵（Matrix）是很多科学计算问题研究的对象，矩阵可以用二维数组来表示。

图最直观的一种存储方法就是，邻接矩阵（Adjacency Matrix）。

In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

定义如下：

设 $G=(V,\ E)$ 是一个图，其中 $V={v_0,\ v_1,\ …\ ,\ v_{n-1}}$，那么 $G$ 的邻接矩阵 $A$ 定义为如下的 $n$ 阶方阵：

$$
A_{[i][j]}=
\begin{cases}
1& {若\ (v_i,\ v_j)\ 或\ <v_i,\ v_j>\ ∈\ E}\
0& {若\ (v_i,\ v_j)\ 或\ <v_i,\ v_j>\ ∉\ E}
\end{cases}
$$

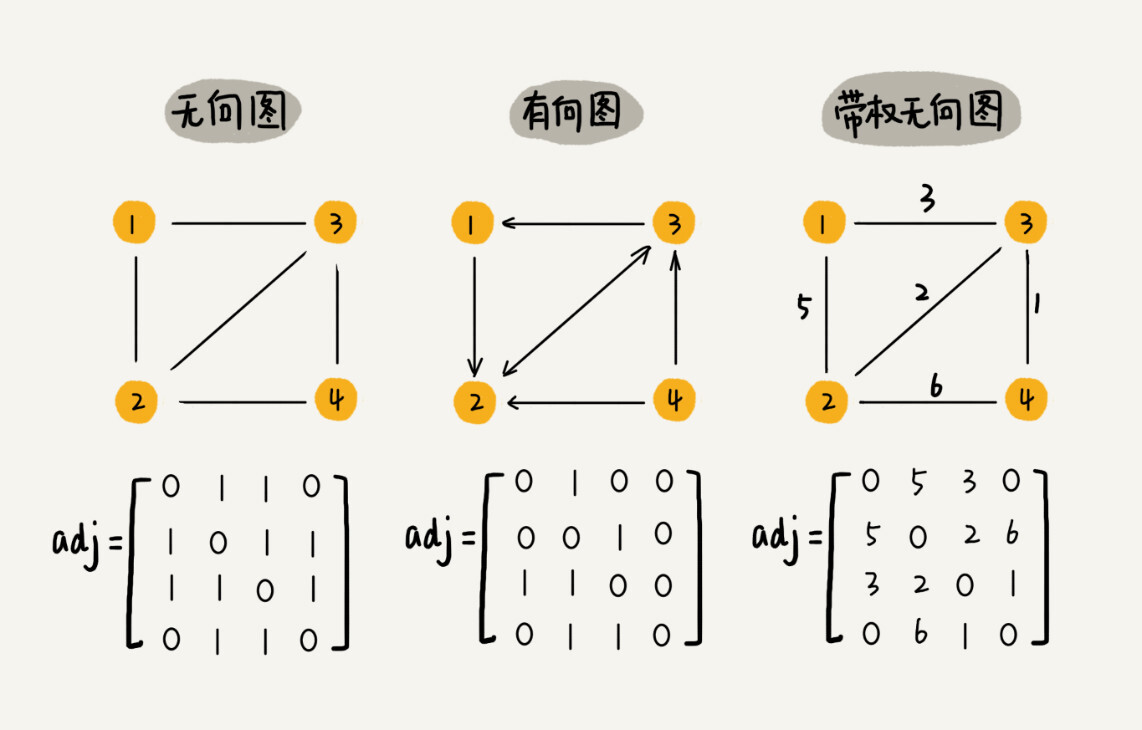
可见，若无向图 $G$ 中有 $n$ 个顶点 $m$ 条边，采用邻接矩阵存储，则该矩阵中非 0 元素的个数为：
$$
2m
$$

对称矩阵（Symmetric Matrix）

用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间。为什么这么说呢？

对于无向图来说，如果 $A_{[i][j]}$ 等于 1，那 $A_{[j][i]}$ 也肯定等于 1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。

上面描述的是一类特殊矩阵：

若一个 $n$ 阶方阵 $A$ 中的元素满足下述条件：
$$
a_{ij}=a_{ji} \quad (0≤i,\ j≤n-1)
$$

则 $A$ 称为对称矩阵（Symmetric Matrix）。

In the mathematical discipline of linear algebra, a symmetric matrix is a square matrix that is equal to its transpose.

对称矩阵可以压缩存储：对称矩阵有近一半的元素可以通过其对称元素获得，为每一对对称元素只分配一个存储单元，则可将 $n^2$ 个元素压缩存储到含有 $n(n＋1)/2$ 个元素的一维数组中。

三角矩阵（Triangular Matrix）

以对称矩阵的主对角线为界，上（下）半部分是一个固定的值（如 0），这样的矩阵称为：上三角矩阵（Upper Triangular Matrix）或下三角矩阵（Lower Triangular Matrix）。

In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix. A square matrix is called lower triangular if all the entries above the main diagonal are zero. Similarly, a square matrix is called upper triangular if all the entries below the main diagonal are zero.

稀疏矩阵（Sparse Matrix）

如果我们存储的是稀疏矩阵（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就三五百个而已。如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了。

这里描述的是一类「非零元素个数很少的矩阵」，即稀疏矩阵（Sparse Matrix）。

In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero.

稀疏矩阵可以压缩存储，使用三元组表示法：$(i,\ j,\ a_{ij})$。

---

总结，邻接矩阵的存储方法的优点：

• 首先，邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点的关系时，就非常高效。
• 其次，用邻接矩阵存储图的另外一个好处是方便计算。这是因为，用邻接矩阵的方式存储图，可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个 Floyd-Warshall 算法，就是利用矩阵循环相乘若干次得到结果。参考：《矩阵运算及其运算规则》

此外，针对邻接矩阵比较浪费存储空间的缺点，解决方案：

• 不带权的无向图的邻接矩阵，一定是一个对称矩阵，因此可以转为三角矩阵之后进行压缩存储。
• 有向图、带权图的邻接矩阵，一般都不是一个对称矩阵。但如果是一个稀疏矩阵，可以使用三元组表示法进行压缩存储。

邻接表（Adjacency List）

邻接表（Adjacency List） 的定义：

In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.

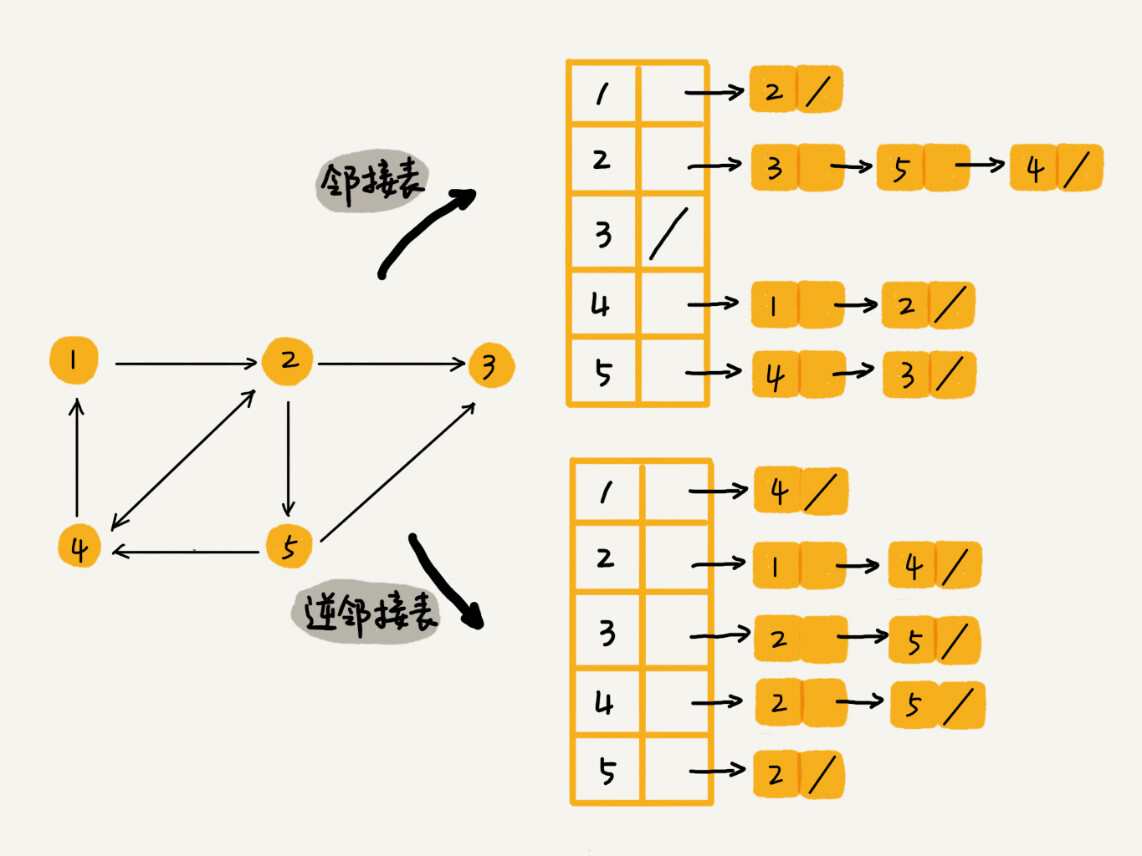
还记得我们之前讲过的时间、空间复杂度互换的设计思想吗？邻接矩阵存储起来比较浪费空间，但是使用起来比较节省时间。相反，邻接表存储起来比较节省空间，但是使用起来就比较耗时间。

就像图中的例子，如果我们要确定，是否存在一条从顶点 2 到顶点 4 的边，那我们就要遍历顶点 2 对应的那条链表，看链表中是否存在顶点 4。而且，我们前面也讲过，链表的存储方式对缓存不友好。所以，比起邻接矩阵的存储方式，在邻接表中查询两个顶点之间的关系就没那么高效了。

在基于链表法解决冲突的散列表中，如果链过长，为了提高查找效率，我们可以将链表换成其他更加高效的数据结构，比如平衡二叉查找树等。所以，我们也可以将邻接表同散列表一样进行 “改进升级”。

我们可以将邻接表中的链表改成平衡二叉查找树。实际开发中，我们可以选择用红黑树。这样，我们就可以更加快速地查找两个顶点之间是否存在边了。当然，这里的二叉查找树可以换成其他动态数据结构，比如跳表、散列表等。除此之外，我们还可以将链表改成有序动态数组，可以通过二分查找的方法来快速定位两个顶点之间否是存在边。

图的应用

图的搜索（遍历）

https://en.wikipedia.org/wiki/Graph_traversal

图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。具体方法有很多，比如两种最简单、最 “暴力” 的深度优先、广度优先搜索，还有 A*、IDA* 等启发式搜索算法。

连通图的两种搜索方式：

	邻接矩阵	邻接表
深度优先搜索		栈（LIFO）实现（$O(n+e)$）
广度优先搜索		队列（FIFO）实现

深度优先搜索（DFS）

https://en.wikipedia.org/wiki/Depth-first_search

深度优先搜索（Depth-first search, DFS）类似于树的先序遍历。

想象成“走迷宫”的过程。

实际上，深度优先搜索用的是一种比较著名的算法思想——回溯思想。这种思想解决问题的过程，非常适合用递归来实现。而递归的本质就是压栈与出栈操作。

深度优先搜索的栈（LIFO）实现，过程如下图，将压栈 push 的顶点序列输出即可。

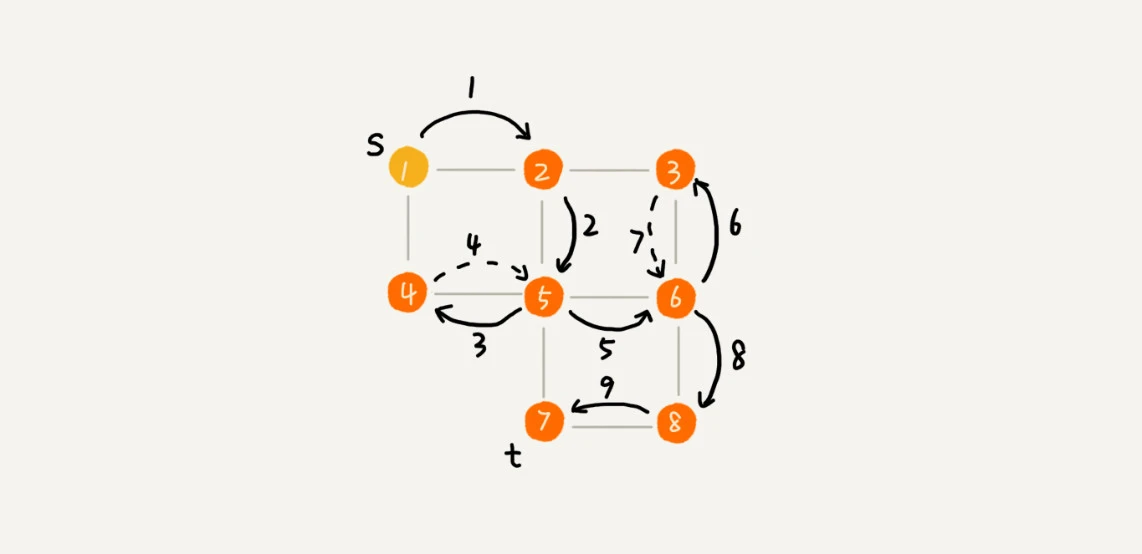
广度优先搜索（BFS）

https://en.wikipedia.org/wiki/Breadth-first_search

广度优先搜索（Breadth-first search, BFS）类似于树的层次遍历。

想象成 “地毯式搜索” 层层推进的过程。

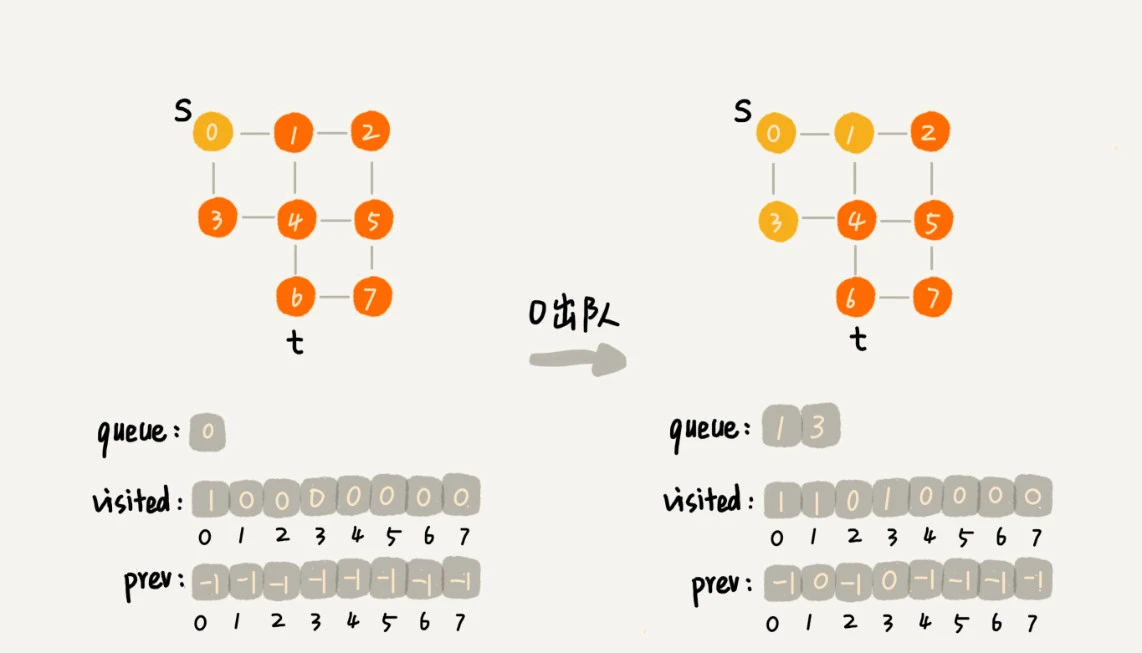
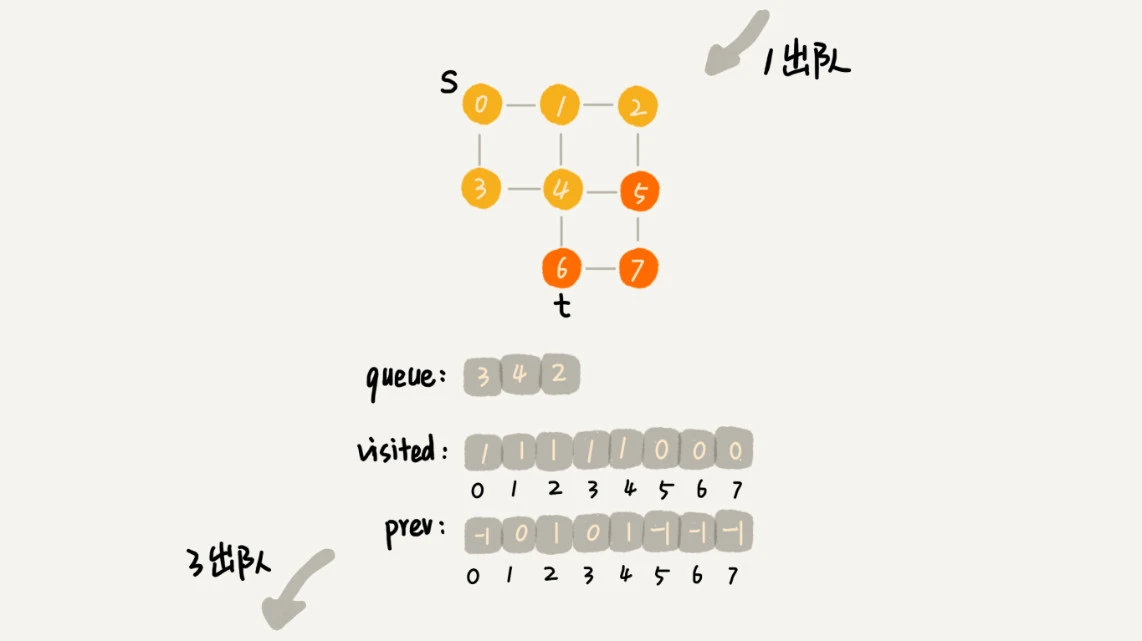
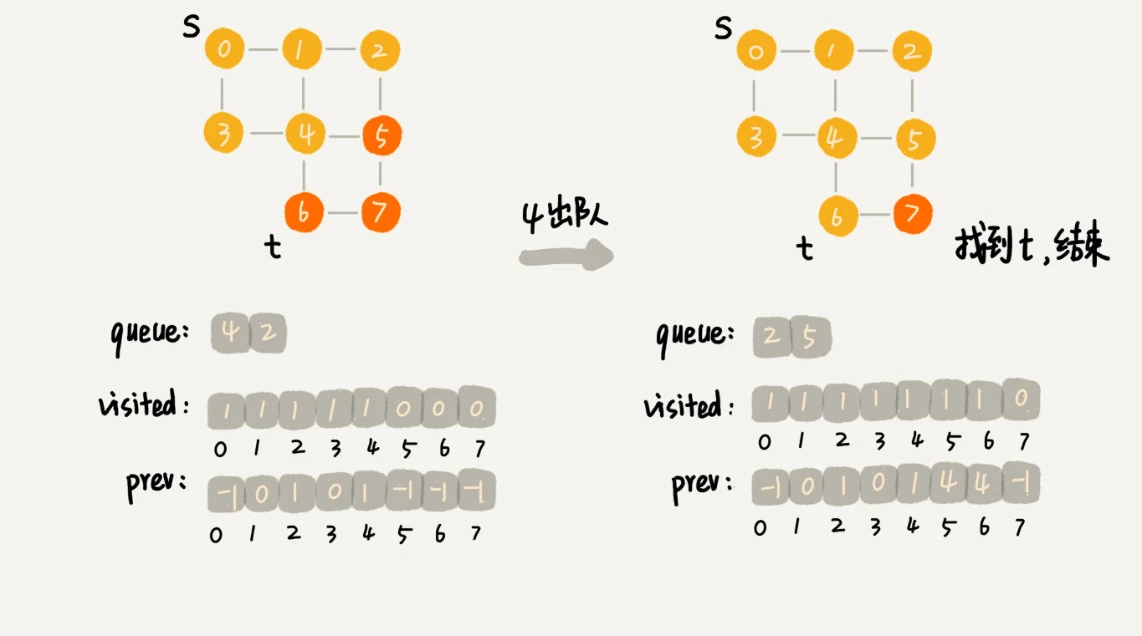
广度优先搜索的队列（FIFO）实现，过程如下：

1. 首先顶点入队，并输出。

2. 然后顶点出队。

3. 将出队顶点相连的所有顶点依次入队，并输出。

重复 2、3 两步，直到所有顶点输出为止，最终结果不唯一。

连通分量

无向图中的极大连通子图（Maximal connected subgraph）称为原图的连通分量（Connected Components）。

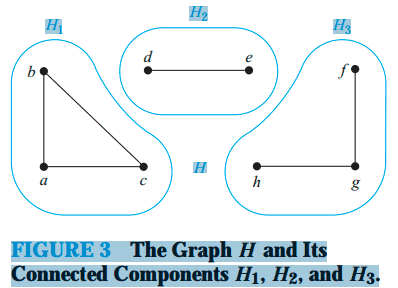
连通图只有一个极大连通子图，就是它本身。

最小生成树问题（MST problem）

如果无向图中，任意两个顶点都连通，称为连通图（Connected Graph）。如下图：

如果连通图中，边上有权值，称为连通网（Connected Network）。如下图：

连通图的一次遍历所经过的点和边的集合，构成一棵生成树（Spanning Tree）。

一个连通图的生成树，是含有该连通图的全部顶点的一个极小连通子图（Minimum connected subgraph）。

一个具有 $n$ 个顶点的连通图，它的生成树的边数为 $n-1$。

连通图的遍历序列不是唯一的，所以能得到不同的生成树。其中权值总和最小的生成树，称为最小生成树（Minimum Spanning Tree, MST）。如下图：

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible.

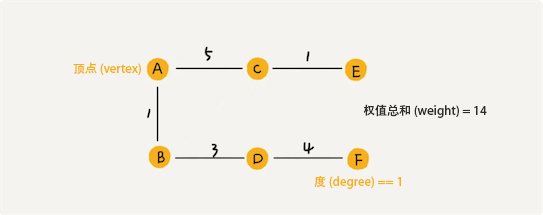
最小生成树的准则：

• 必须使用且仅使用连通网中的 n-1 条边来联结网络中的 n 个顶点；
• 不能使用产生回路的边；
• 各边上的权值总和达到最小。

最小生成树的应用：规划出总长度最小的网络

• 例如工程领域设计，如最小成本的铺设网线、电缆、管道、道路、…
• https://en.wikipedia.org/wiki/Minimum_spanning_tree#Applications

Prim 算法

https://en.wikipedia.org/wiki/Prim%27s_algorithm

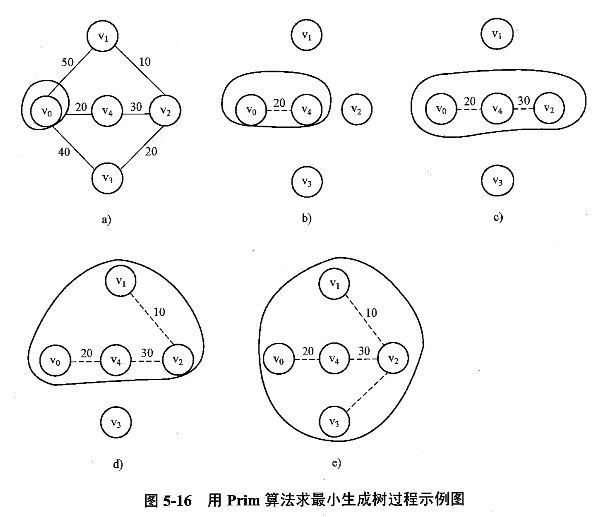
假设 $N=(V,\ E)$ 是连通网，$TE$ 是 $N$ 上最小生成树中边的集合：

1. 初始态：$U={u_0},\ (u_0∈V),\ TE={}$

2. 在所有 $u∈U,\ v∈V-U$ 的边 $(u,\ v)∈E$ 中找一条代价最小的边 $(u,\ v_0)$ 并入集合 $TE$，
   同时 $v_0$ 并入 $U$

3. 重复 2，直到 $U=V$

形象化理解：由点找边再找点的过程。

---

📝 习题 📝

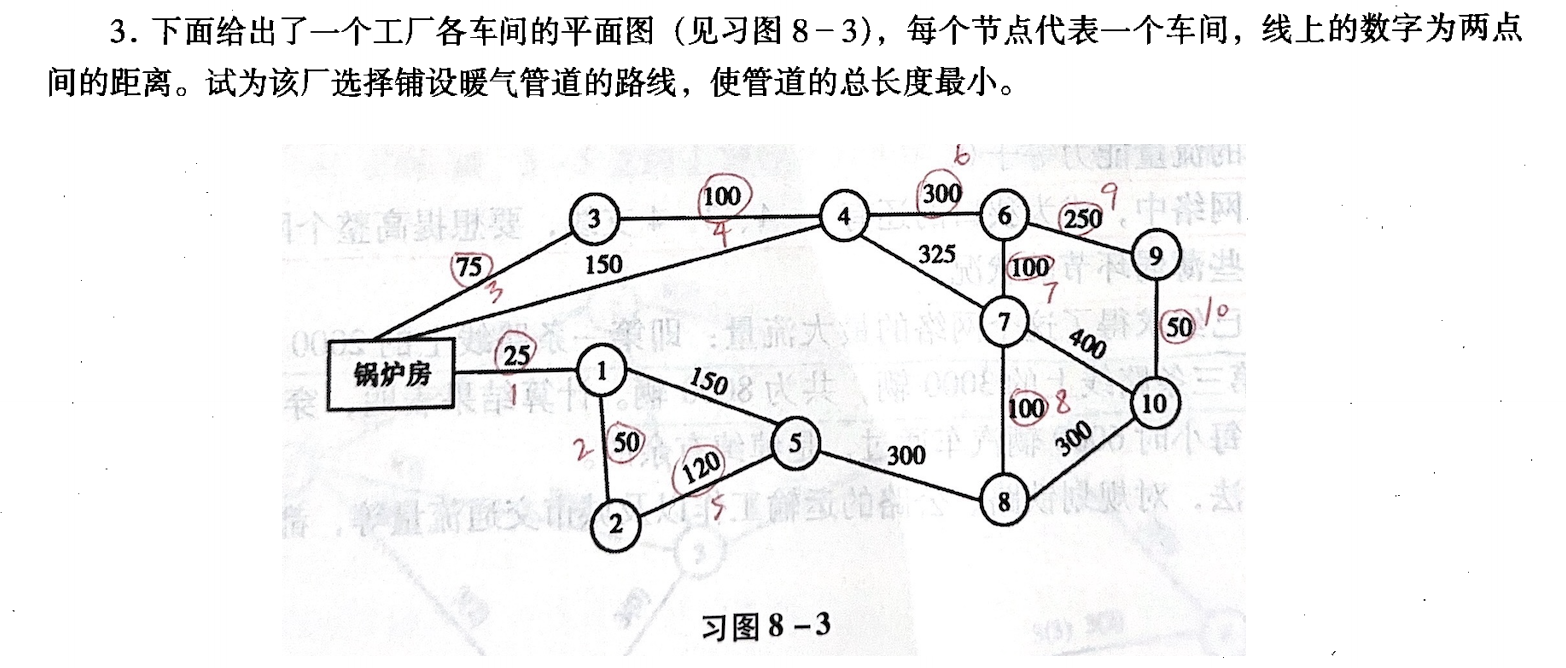
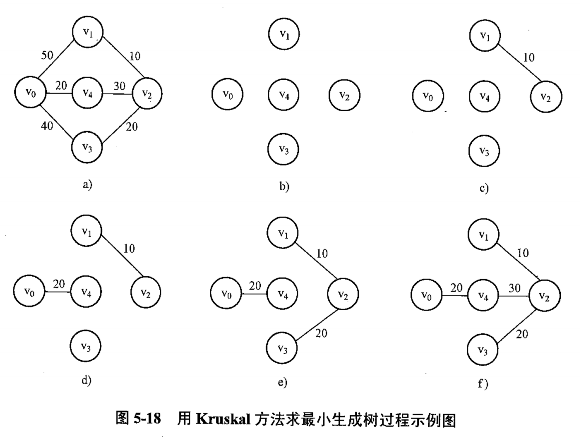
Kruskal 算法（加边法）

https://en.wikipedia.org/wiki/Kruskal%27s_algorithm

假设 $N=(V,\ E)$ 是连通网

1. 非连通图 $T={V,\ {}}$，图中每个顶点自成一个连通分量
2. 在 $E$ 中找一条代价最小，且其两个顶点分别依附不同的连通分量的边（即不形成回路的边），将其
   加入 $T$ 中
3. 重复 2，直到 $T$ 中所有顶点都在同一连通分量上

形象化理解：由边找点。

最短路径问题（Shortest path problem）

在图论中，最短路径问题是在连通图中寻找两个顶点之间的一条路径，使得其组成边的权重（如时间、距离、费用等）之和最小化的问题。

最短路径的应用：

• 例如规划交通路线、解决运输问题、编制生产计划、…
• https://en.wikipedia.org/wiki/Shortest_path_problem#Applications

最短路径的计算方法：

最短路径算法还有很多，比如 Bellford 算法、Floyd 算法等等。

回溯算法

从终点开始，逐步逆向推算。（从终点到起点的逆向回溯过程。）

Dijkstra 算法

https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm

《44 | 最短路径：地图软件是如何计算出最优出行路径的？》

---

📝 习题 📝

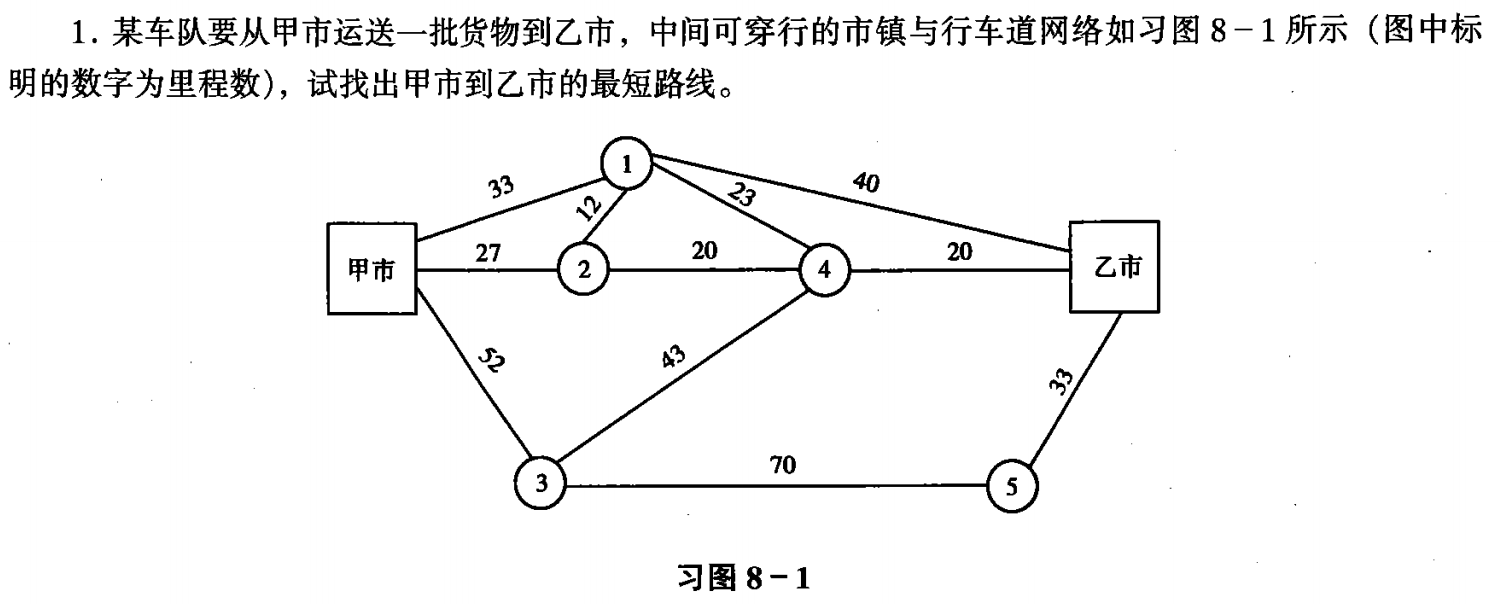
目的地	起点：甲	前驱	最短路径
1 ✅（2️⃣）	33	甲	甲 - 1
2 ✅（1️⃣）	27	甲	甲 - 2
3 ✅（4️⃣）	52	甲	甲 - 3
4 ✅（3️⃣）	47	2	甲 - 2 - 4
5 ✅（6️⃣）	122 100	3 乙	甲 - 2 - 4 - 乙 - 5
乙 ✅（5️⃣）	73 67	1 4	甲 - 2 - 4 - 乙

A* 算法

https://en.wikipedia.org/wiki/A*_search_algorithm

《49 | 搜索：如何用 A * 搜索算法实现游戏中的寻路功能？》

最大流问题（Maximum flow problem）

https://en.wikipedia.org/wiki/Maximum_flow_problem

当以物体、能量或信息等作为流量流过网络时，怎样使流过网络的流量最大，或者使流过网络的流量的费用或时间最小。通常，把设计这样的流量模型问题，叫作网络的流量问题。

最大流量问题，就是在一定条件下，要求流过网络的流量为最大的问题。

---

📝 习题 📝

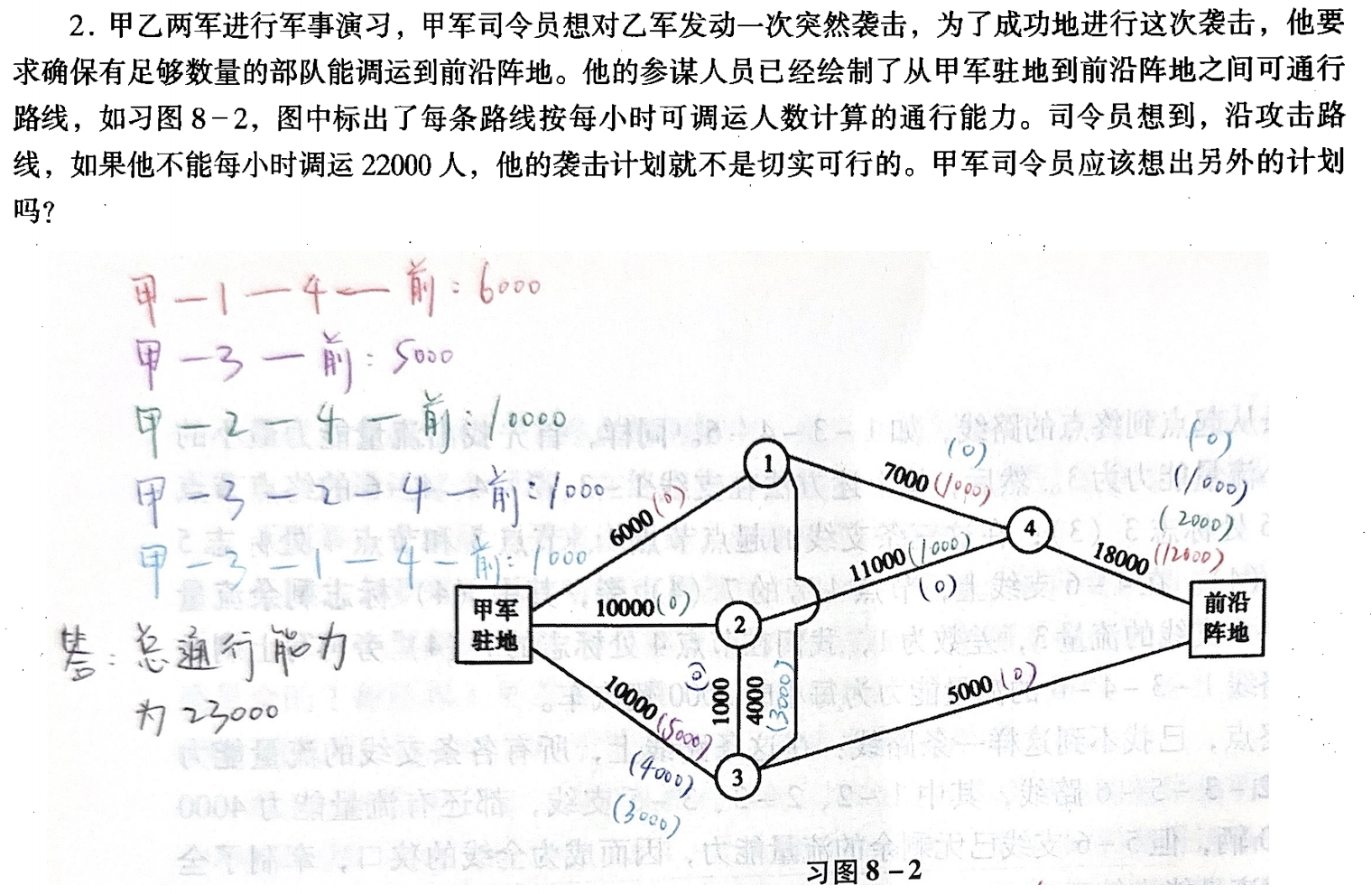
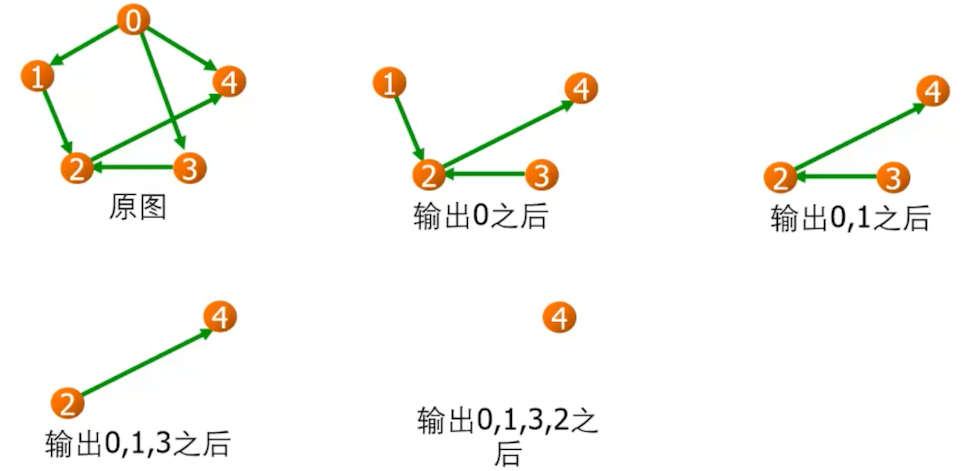
拓扑排序（Topological sorting）

拓扑排序算法：

1. 在有向图中选一个入度为 0 的顶点并输出。
2. 从图中删除该顶点和所有以它为尾的弧。

重复 1、2 两步，直到所有顶点输出为止，最终结果不唯一。

设某有向图中有 n 个顶点和 e 条边，进行拓扑排序时，总的计算时间为 $O(n+e)$。

https://en.wikipedia.org/wiki/Topological_sorting

《43 | 拓扑排序：如何确定代码源文件的编译依赖关系？》

社交网络（Social network）

图的两种存储结构，在社交应用的优缺点对比如下。例如在微博（有向图）中，设我为 $v_i$，ta 为 $v_j$：

• 邻接矩阵
  • 优点：
    • 存储方式简单、直接，因为基于数组，用户之间的关系获取（$O(n)$）、建立（$O(1)$）、查找（$O(1)$）非常高效。
  • 缺点：
    • 比较浪费存储空间。
    • 获取的好友关系无序。
• 邻接表：
  • 优点：
    • 节约存储空间。
    • 获取的好友关系可以按关键字排序。
  • 缺点：
    • 用户之间的关系建立、查找相对低效（取决于”关系“使用的数据结构）。
    • 关注列表（邻接表）、粉丝列表（逆邻接表）需要分别存储、同时维护，关系维护相对繁琐。

需求	邻接矩阵	邻接表 A、逆邻接表 R
我关注的人	$A_{[i][0-n]}$	$A_{[i]}$
我的粉丝（关注我的人）	$A_{[0-n][i]}$	$R_{[i]}$
我关注 ta	$A_{[i][j]}$ = 1	insert($A_{[i]}$, $v_j$) && insert($R_{[j]}$, $v_i$)
我取消关注 ta	$A_{[i][j]}$ = 0	delete($A_{[i]}$, $v_j$) && delete($R_{[j]}$, $v_i$)
我是否关注 ta	$A_{[i][j]}$ == 1	exist($A_{[i]}$, $v_j$)
ta 的粉丝是否有我	$A_{[i][j]}$ == 1	exist($R_{[j]}$, $v_i$)

基于上述存储结构，可以进一步实现如下需求（以邻接表为例）：

# 求共同关注
A[i] ∩ A[j]

# 我关注的人也关注 ta
foreach(member in A[i]) {
  # 我每个关注的人，他们关注的人中，是否有 ta
  A[member] ∩ vj
}

# 我可能认识的人
foreach(member in A[i]) {
  # 我每个关注的人，他们关注的人中，有我还没关注的
  A[member] - A[i]
}

《图应用：微博系统中的好友关系》

知识图谱（Knowledge graph）

https://en.wikipedia.org/wiki/Knowledge_graph

参考

https://en.wikipedia.org/wiki/Graph_theory

https://en.wikipedia.org/wiki/Network_theory

《30 | 图的表示：如何存储微博、微信等社交网络中的好友关系？》

《31 | 深度和广度优先搜索：如何找出社交网络中的三度好友关系？》