数据结构系列(一)概论总结
引言
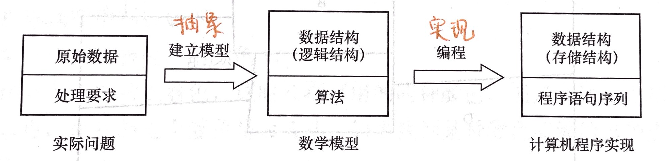
计算机解决一个具体问题时,一般需要经过以下几个步骤:
- 从具体的问题抽象出一个适当的数学模型;什么是数学模型呢?数学模型常常是现实世界的一个简化,是抽取对象的本质特性构造出来的。尽管数学是一门精准的科学,但是我们建立数学模型却要从实际出发,要针对问题做必要简化,简化的标准有两个:够用、易解。
- 设计一个求解该数学模型的算法;
- 用某种计算机编程语言编写实现该算法的程序,调试和运行程序直至最终得到问题的解。
基本概念和术语

- 数据:所有被计算机存储、处理的对象。
- 数据对象:是性质相同的数据元素的集合,是数据的子集。
- 数据元素:数据的基本单位,也是运算的基本单位。例如在数据库中,又称为记录(Record)/元组(Tuple)。
- 数据项:数据不可分割的最小单位。例如在数据库中,又称为字段(Field)/域(Domain)。
- 数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。它包括:
- 数据的逻辑结构
- 数据的存储结构
- 数据的基本运算
逻辑结构
https://en.wikipedia.org/wiki/Abstract_data_type
- https://en.wikipedia.org/wiki/Set_(abstract_data_type)
- https://en.wikipedia.org/wiki/List_(abstract_data_type)
- https://en.wikipedia.org/wiki/Tree_(data_structure)
- https://en.wikipedia.org/wiki/Graph_(abstract_data_type)
集合结构
任意两个结点之间都没有邻接关系,组织形式松散:
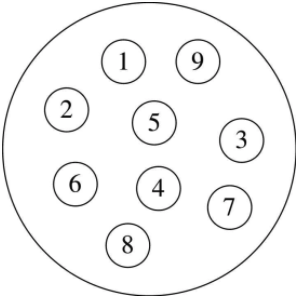
集合的三大特性:
- 确定性:给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
- 互异性:一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
- 无序性:一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
集合之间可以进行运算:
| 数学符号 | 含义 | 英文 |
|---|---|---|
| ∩ | 交 | Intersection |
| ∪ | 并 | Union |
| − | 差 | Difference |
集合的实现:
- 无序集合:散列表
- 有序集合:BST
线性结构
顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。
而与它相对立的概念是非线性表,比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,数据之间并不是简单的前后关系。
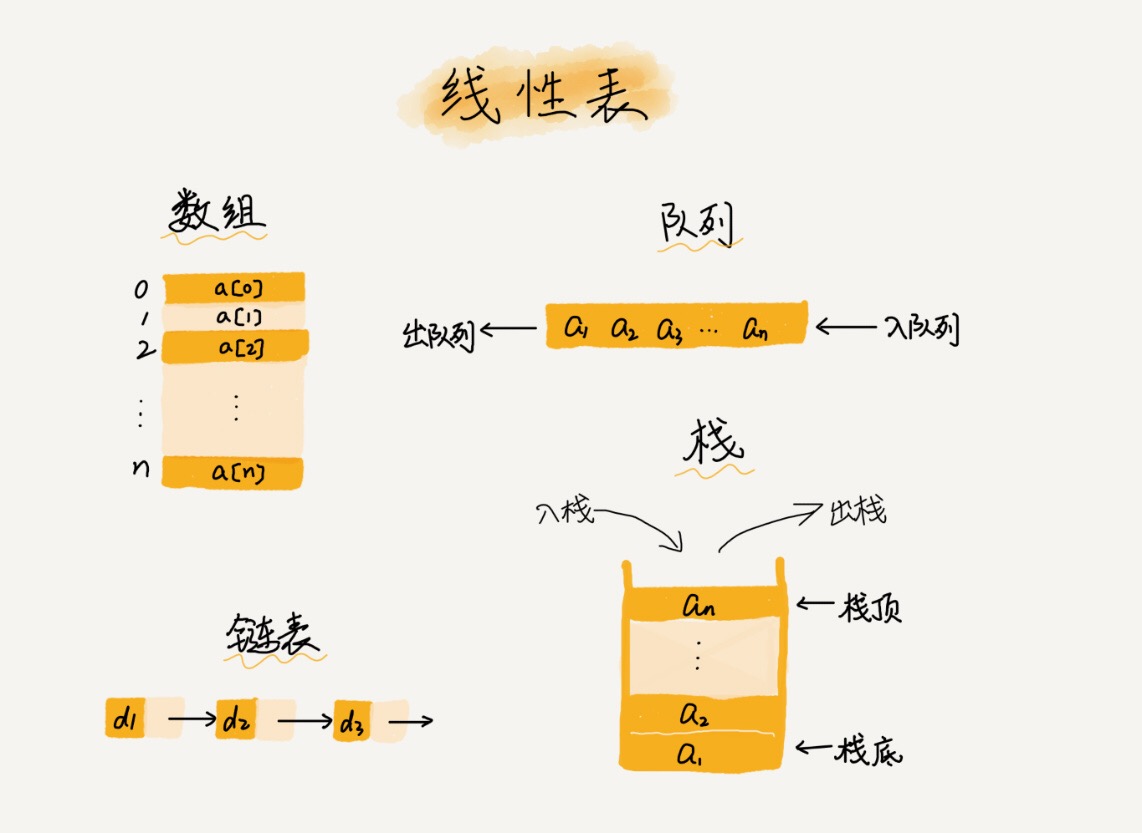
特征:
- 排队(1:1)
- 起始节点无直接前驱
- 终端节点无直接后继
- 中间节点都有直接前驱和直接后继
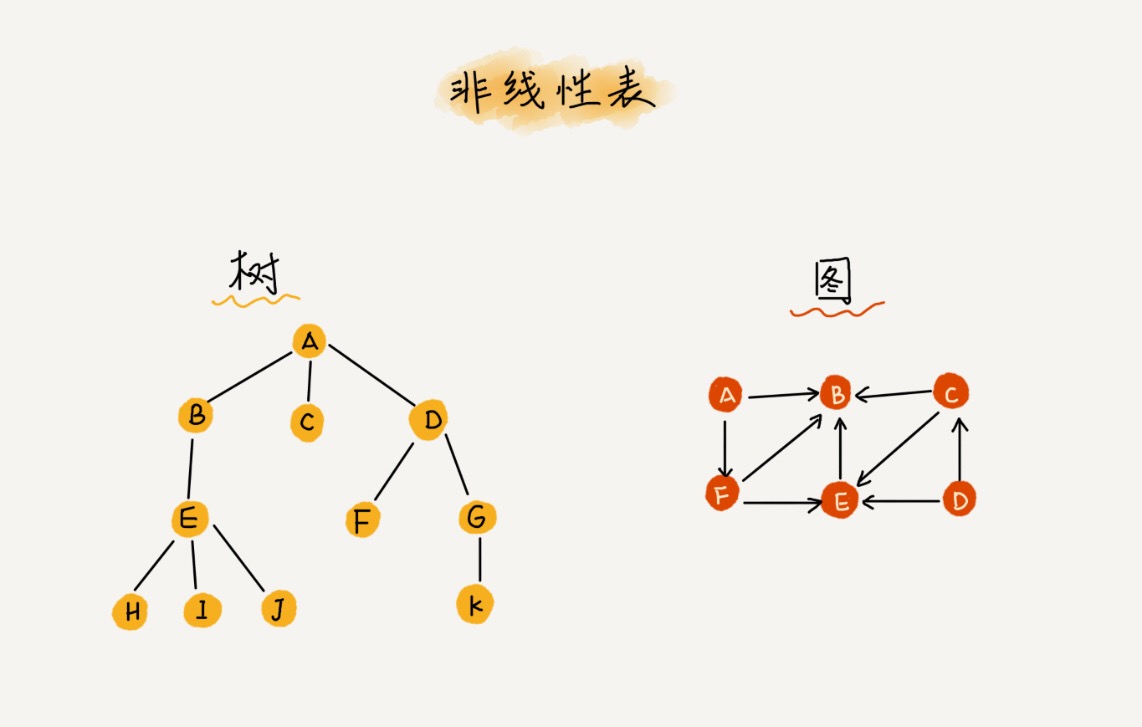
树形结构
父子(1:N)
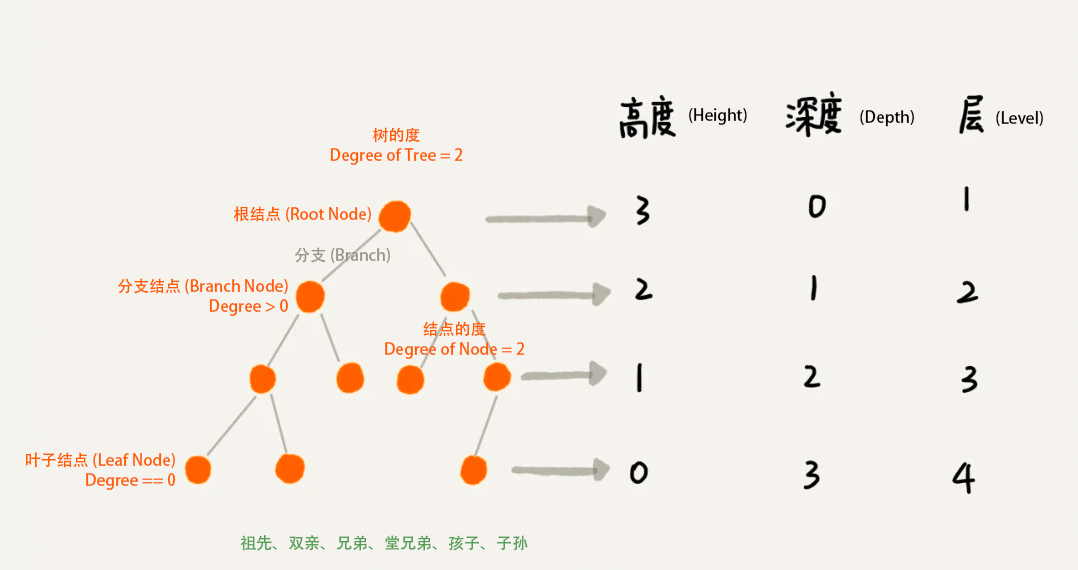
有没有想过为啥只有二叉树,而没有一叉树?实际上链表就是特殊的树,即一叉树。
图结构
地图(N:M)
存储结构
数据的逻辑结构在计算机中的实现,称为数据的存储结构(或物理结构)。
一般情况下,一个存储结构包括以下两个部分:
- 存储数据元素本身
- 数据元素之间的关联方式
逻辑结构常见的存储结构实现如下:
| 顺序存储方式 | 链式存储方式 | 散列存储方式 | 索引存储方式 | |
|---|---|---|---|---|
| 集合结构 | 散列表(Hash Table) | |||
| 线性结构 | 数组(一维、二维) 顺序栈 循环队列(取余运算) |
链表(单向/双向、是否循环) 链栈 链队列 |
||
| 树形结构 (二叉树) |
一维数组 |
链表 |
||
| 树形结构 (多叉树) |
双亲表示法(一维数组) | 孩子链表表示法(一维数组 + 单链表) 孩子兄弟表示法(二叉链表,LC-RS) |
||
| 图结构 | 邻接矩阵(二维数组) | 邻接表(一维数组 + 单链表) |
顺序存储方式
所有存储结点存放在一个连续的存储区中。利用结点在存储区中的相对位置来表示数据元素之间的逻辑关系。
链式存储方式
每个存储结点除了含有一个数据元素之外,还包含指针,每个指针指向一个与本结点有逻辑关系的结点。利用指针表示数据元素之间的逻辑关系。
散列存储方式
散列表(Hash Table)。
索引存储方式
基本运算
基本运算,是指在某种逻辑结构上施加的操作,即对逻辑结构的加工。这种加工以数据的逻辑结构为对象。一般而言,在每个逻辑结构上,都定义了一组基本运算,这些运算包括:等。
- 建立(Init)
- 读取(Access)
- 查找(Search)
- 插入(Insert)
- 删除(Delete)
算法
定义:一个算法规定了求解给定问题所需的处理步骤及其执行顺序,使得给定问题能在有限时间内被求解。
算法分析:
- 正确性
- 易读性
- 健壮性
- 时空性
时间复杂度

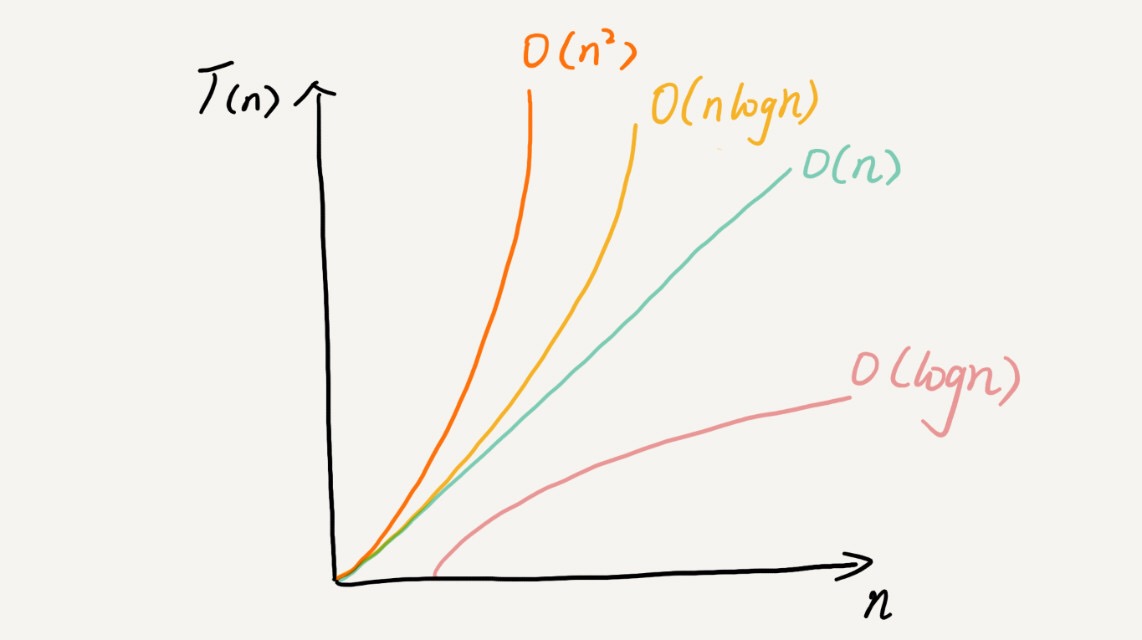
空间复杂度
常用数据结构
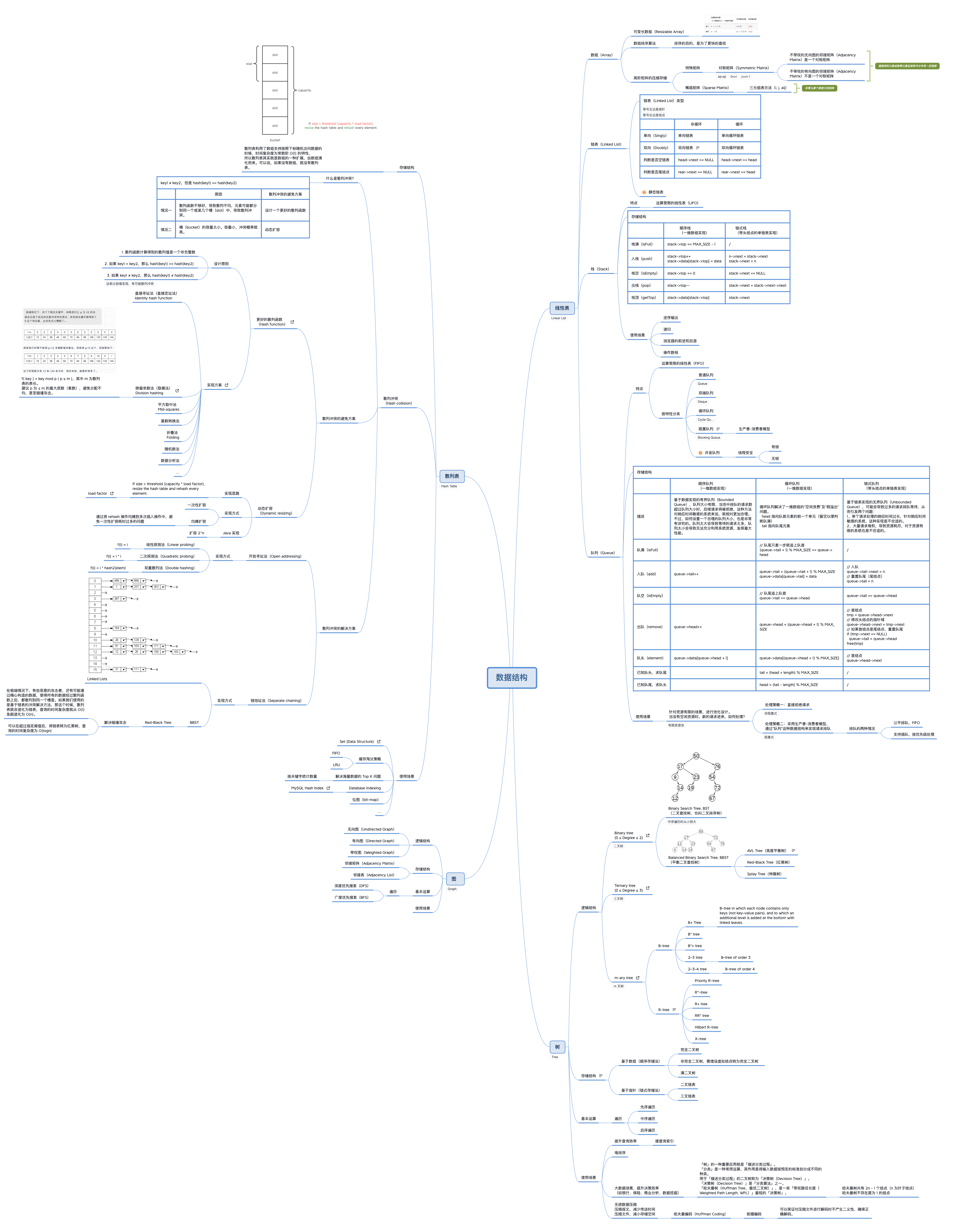
参考
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html