位运算及使用场景总结

发表于 更新于
二进制位运算 十进制运算
& 按位与（AND） $M\&(n-1)$ $M \bmod n$
| 按位或（OR）
~ 按位非（NOT）
^ 按位异或（XOR）
<< 左位移（LEFT SHIFT） $M<<n$ $M*2^n$
>> 右位移（RIGHT SHIFT） $M>>n$ $M/2^n$
>>> 无符号右移

https://en.wikipedia.org/wiki/Mask_(computing)

Using a mask (bitmask) can be set

  • either on or off,
  • or inverted from on to off (or vice versa)

in a single bitwise operation.

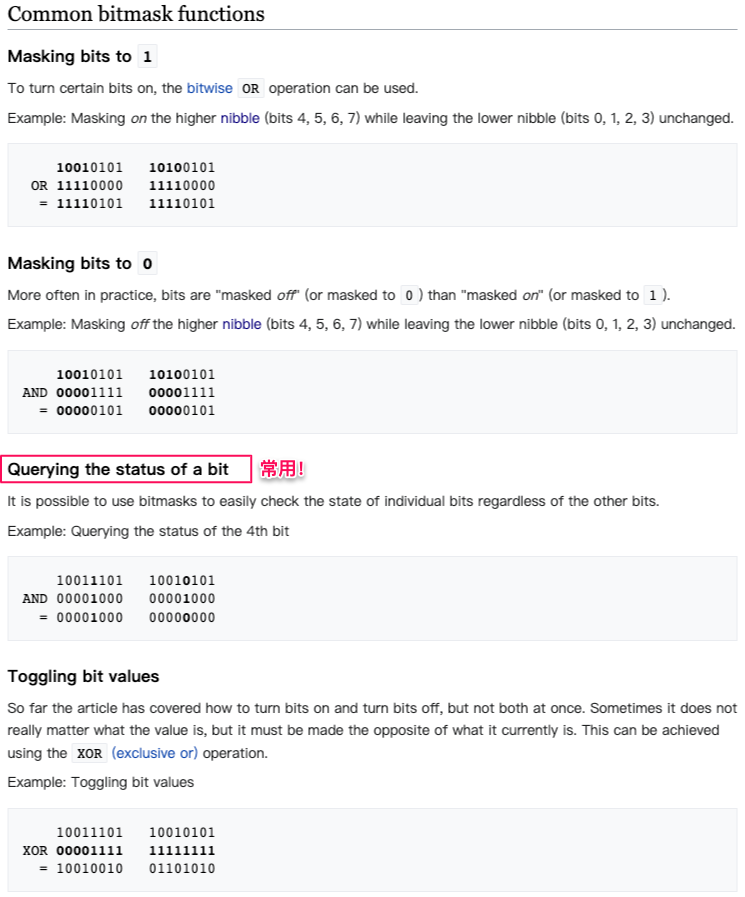
Common bitmask functions

「按位与 &」的使用场景

求子网地址

求子网地址（主机地址与子网掩码做按位与运算），参考：

例子：

Calculate subnet address

Calculate subnet address

实现循环队列

编程的时候，很多时候都会要求一个数在某一个范围内进行反复循环，例如实现循环队列。如果使用 if 语句，当判断达到最大值的时候回到开始处，效率较低。是否有更简单更高效的方法？

  • & 按位与（AND）。比如说我想让一个数在 0-7 内循环，该如何做呢？temp = (temp++)&0x07，如此就简单的实现了 0-7 循环。因为要实现 0-7 的循环，其实只要提取一个变量递增的低三位即可。不管这个变量如何变化，它的低三位始终都是在 0-7 循环变化的。同理，它也可以实现 0-15、0-31 变化。但是这个方法有局限，它只能按照连续 bit 位的最大值进行循环。
  • % 取余运算（Modulo），它不存在上述限制。可以在 0-任意数循环。比如 0-5 循环，只要 temp = (temp++)%6（注意是 6 而不是 5），那么 temp 就会在 0-5 之间循环了。

「按位或 |」的使用场景

单个变量保存多个值，节省存储空间

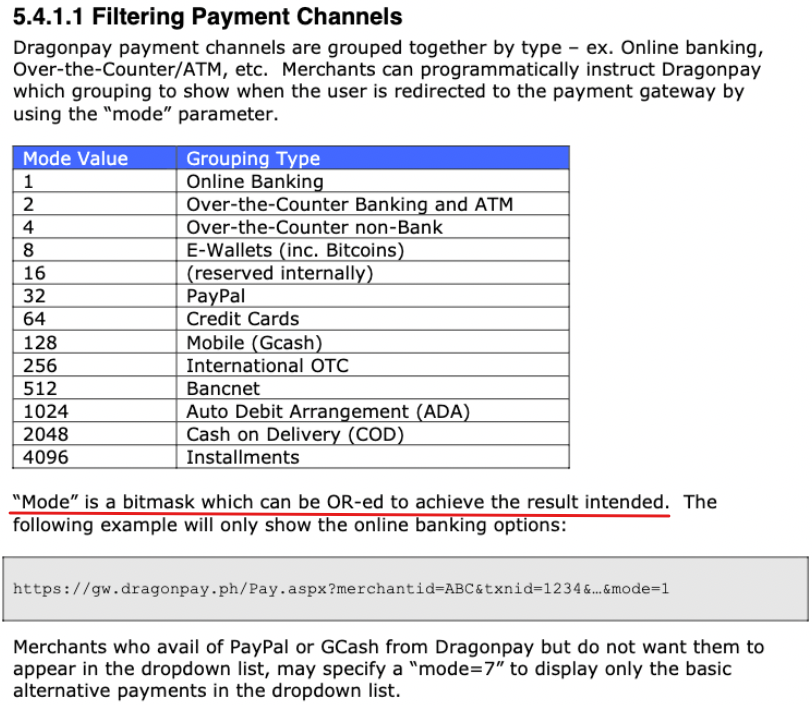
DragonPay

雪花算法的拼接

1
2
3
4
5
     timestamp << TIMESTAMP_SHIFT
| dataCenterNo << DATA_CENTER_NO_SHIFT
    | workerNo << WORKER_NO_SHIFT
       | seqNo << SEQ_NO_SHIFT
         | ext

线程池的成员属性 ctl

线程池的成员属性 ctl，高 3 位表示 runState，低 29 位表示 workerCnt（按位或运算 bitwise OR）：

1
2
3
4
5
6
7
runState workerCnt                       runState workerCnt
     000 00000000000000000000000000000   SHUTDOWN empty
‭‭     001 00000000000000000000000000000       STOP empty
     010 00000000000000000000000000000    TIDYING empty
     ‭011 00000000000000000000000000000‬ TERMINATED empty
     111 00000000000000000000000000000    RUNNING empty
‭     111 11111111111111111111111111111    RUNNING full

操作系统 - 分页存储管理 - 逻辑地址结构

  • 若用 $m$ 位表示逻辑地址，页大小为 $2^n$ 字节，则低 $n$ 位表示「页内偏移量」，高 $m-n$ 位表示「页号」。
  • 例如 32 位的逻辑地址中，页大小为 $2^{12}$ (4KB)，则低 12 位表示「页内偏移量」，高 20 位表示「页号」。即：可用内存为「页号量 $2^{20}$」×「页大小 $2^{12}$ B」=「$2^{32}$ B」=「4 GB」

paging address structure

epoll_ctl() 的 event 参数

1
2
3
4
EPOLLIN | EPOLLOUT | EPOLLRDHUP | EPOLLPRI | EPOLLERR | EPOLLHUP | EPOLLET | EPOLLONESHOT

event.events = EPOLLIN | EPOLLET;
epoll_ctl (efd, EPOLL_CTL_ADD, sfd, &event);

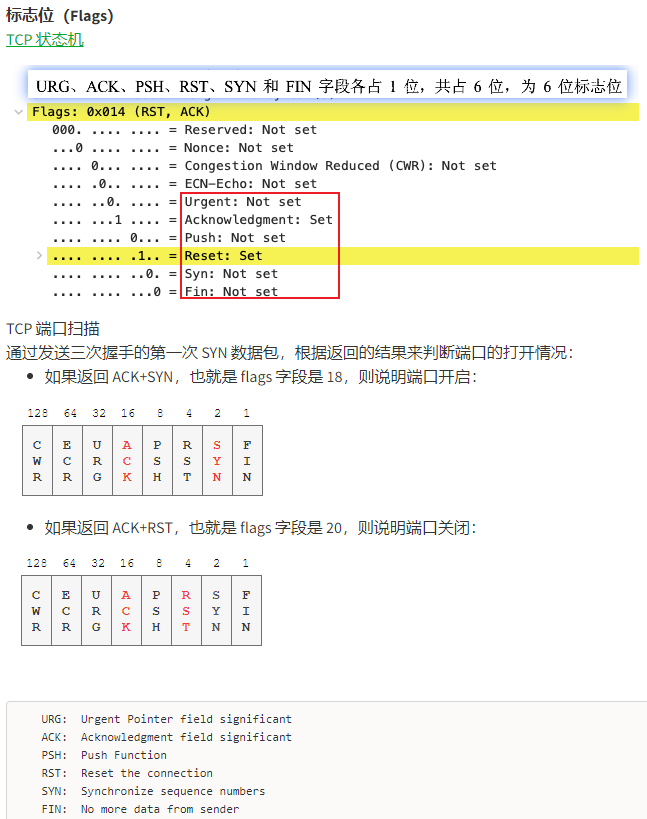
TCP - Header Format - Flags

TCP - Header Format - Flags

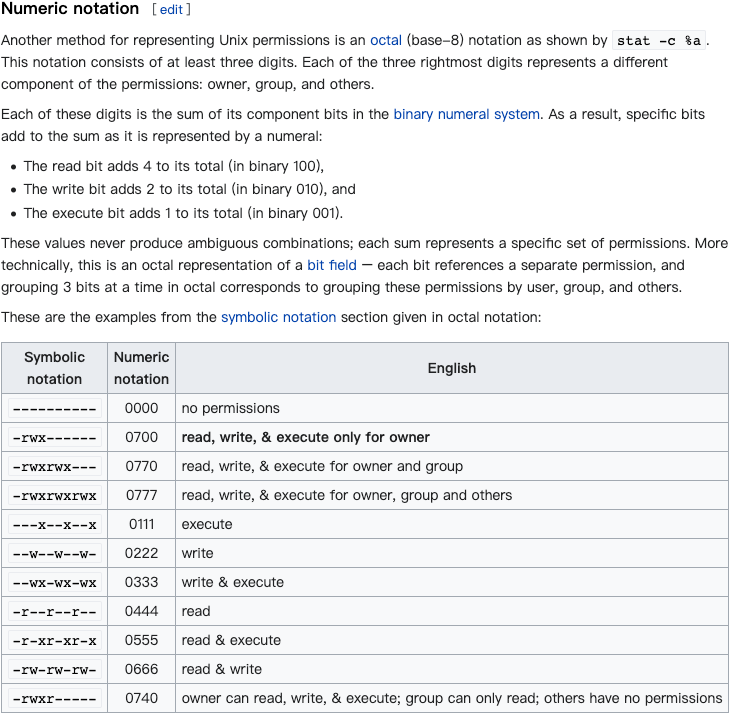
Unix-like permissions

chmod、umask

Unix-like permissions

「按位异或 ^」的使用场景

《异或运算 XOR 使用场景 | 阮一峰》

前向纠错（FEC)）

TCP 协议实现可靠数据传输的 5 种措施中之一——差错控制，有两种纠错方案：

其中 FEC 的实质就是按位异或运算：

FEC

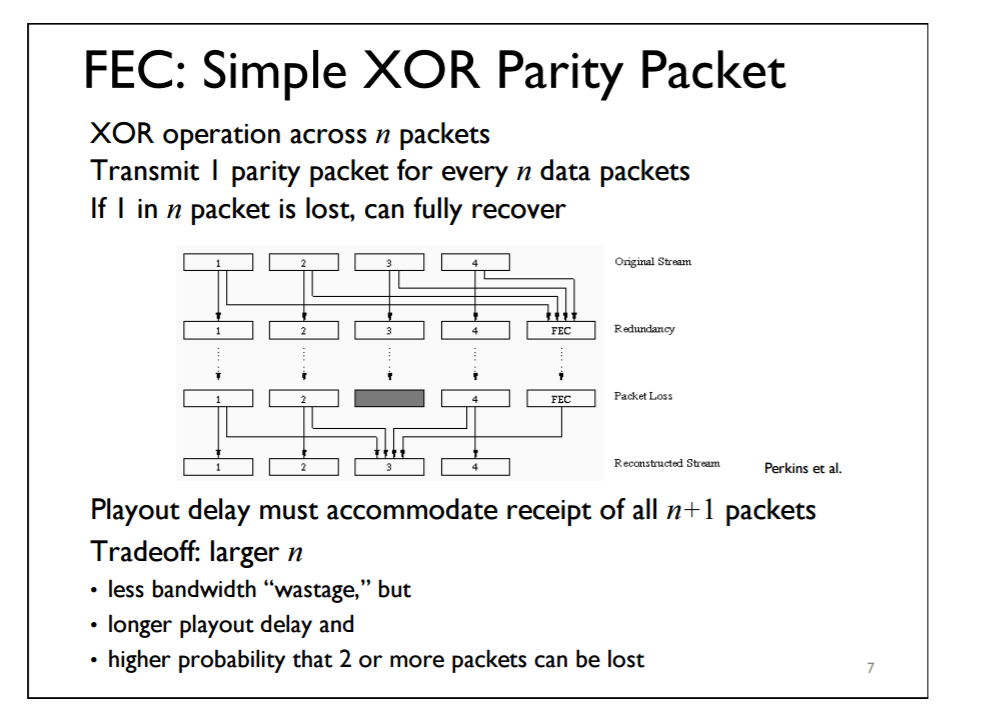
参考：https://www.jianshu.com/p/6157e120ef99

求 hash 值

求 hash 值使用了：

  • >>> 无符号右移
  • ^ 按位异或
  • & 按位与
1
2
3
4
5
int hash(Object key) {
    int h = key.hashCode();
    h = h ^ (h >>> 16);
    return h & (capitity - 1); //capicity 表示散列表的大小
}

位移

逻辑右移可以处理除数为任意二的幂的除法，即：$M>>n$ 等于 $M/2^n$

更一般地，在特定底数 Base 的进位制中，除数（或分母）为任意 $Base^n$ 的除法（n 为整数）皆可以透过将数字位数向右移 n 位来完成。例如 除以十：

$M/Base^n$ Base 2 Base 8 Base 10 Base 16
230 / 2 = 115 1110 0110 / 10 = 111 0011
230 / 8 = 28 346 / 10 = 34
230 / 10 = 23 230 / 10 = 23
230 / 16 = 14 0xE6 / 10 = 0xE

参考

https://en.wikipedia.org/wiki/Bit

https://en.wikipedia.org/wiki/Bitwise_operation

https://en.wikipedia.org/wiki/Bit_array

https://dev.mysql.com/doc/refman/5.7/en/bit-functions.html

《计算机中有哪些令人拍案叫绝的设计？ | 良许 Linux》

《C 语言”位运算”有哪些奇特技巧？》